副題
1. 浮動小数点演算の精度
現在、主流のコンピュータ言語は浮動小数点数を表現するための IEEE 754 標準に従っており、Rust 言語も例外ではありません。 Rust言語における倍精度浮動小数点型f64とコンピュータにおけるバイナリデータの格納形式は以下のとおりです。
写真
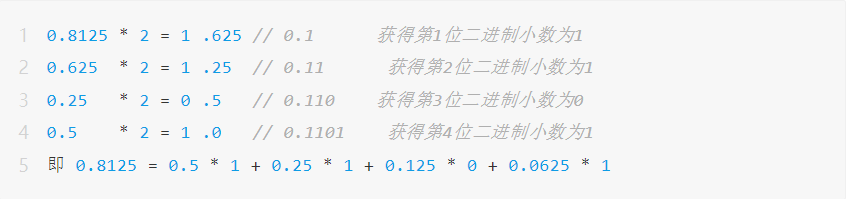
浮動小数点数は、2 を基数とする科学表記法で表されます。たとえば、桁数が限られている 2 進数 0.1101 は、10 進数 0.8125 を表すために使用できます。具体的な変換方法は次のとおりです。
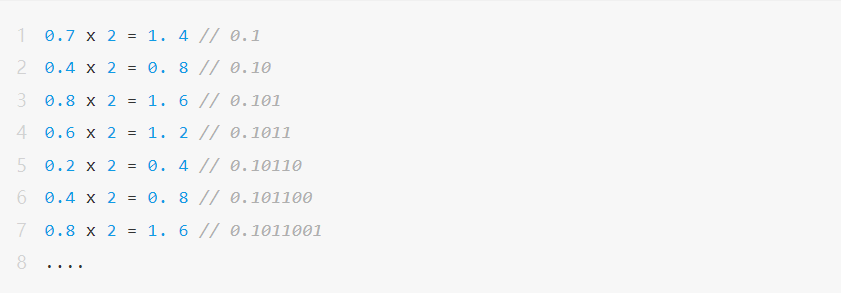
ただし、別の 10 進数 0.7 の場合、実際に浮動小数点数に変換する過程で次の問題が発生します。
つまり、10進数の0.7は0.101100110011001100....(無限ループ)と表現されてしまい、有限ビット長の浮動小数点数では正確に表現できず、「丸め(Rounding)」という現象が発生します。 。

NEAR パブリック チェーン上で、0.7 個の NEAR トークンを 10 人のユーザーに配布する必要があると仮定すると、各ユーザーに配布される NEAR トークンの特定の数が計算され、result_0 変数に保存されます。

このテスト ケースを実行すると、出力は次のようになります。
上記の浮動小数点計算では、amount の値が正確に 0.7 を表しているわけではなく、非常に近似した値 0.69999999999999995559 であることがわかります。さらに、量/除数などの単一の除算演算の場合、演算結果も予期された 0.07 ではなく、不正確な 0.069999999999999999 になります。これは浮動小数点演算の不確実性を示しています。
この点で、スマートコントラクトでは固定小数点数など、他のタイプの数値表現方法を使用することを検討する必要があります。
固定小数点数の小数点の固定位置に応じて、固定小数点数には、固定小数点 (純粋) 整数と固定小数点 (純粋) 小数の 2 種類があります。
数値の最下位桁の後に小数点が固定されている場合、それは固定小数点整数と呼ばれます。
実際のスマート コントラクトの記述では、通常、分母が固定された分数 (分数 ' x/N ' など) が特定の値を表すために使用されます。ここで、 ' N ' は定数であり、 ' x ' は変化する可能性があります。

「N」の値が「1,000,000,000,000,000,000」、つまり「 10^18 」の場合、次のように小数を整数として表すことができます。
NEAR プロトコルでは、N の一般的な値は「 10^24 」です。つまり、10^24 yoctoNEAR は 1 つの NEAR トークンに相当します。
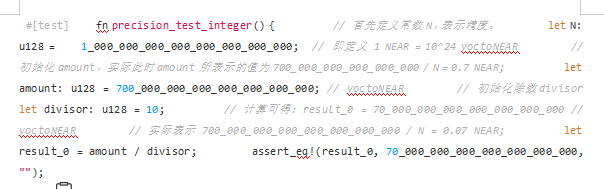
これに基づいて、このセクションの単体テストを次のように計算するように変更できます。

このようにして、数値保険数理計算結果が得られます: 0.7 NEAR / 10 = 0.07 NEAR
2. Rustの整数計算精度の問題
上記のセクション 1 の説明から、整数演算を使用すると、特定の演算シナリオにおける浮動小数点演算の精度の損失の問題を解決できることがわかります。
ただし、これは、整数を使用した計算結果が完全に正確で信頼できることを意味するものではありません。このセクションでは、整数計算の精度に影響を与える理由のいくつかについて説明します。
2.1 操作順序
同じ演算優先度の乗除算の場合、順序の変更が演算結果に直接影響を与え、整数演算精度に問題が生じる可能性があります。

たとえば、次のような操作が存在します。

単体テストの実行結果は次のとおりです。
result_0 = a * c / b と result_1 = (a / b) * c は、計算式は同じですが、結果が異なることがわかります。
分析の具体的な理由は次のとおりです。整数の除算の場合、除数より小さい精度は破棄されます。したがって、result_1 の計算では、最初に計算された (a / b) が計算精度を失って 0 になりますが、result_0 の計算では、最初に a * c の結果が計算され、20_0000 より大きくなります。除数 b よりも大きいため、精度の低下の問題が回避され、正しい計算結果が得られます。

2.2 桁が小さすぎる

この単体テストの具体的な結果は次のとおりです。
計算プロセスの同等の result_0 と result_1 の計算結果は同じではなく、result_1 = 13 が実際の期待される計算値 13.3333.... に近いことがわかります。
3. 数値計算上のRustスマートコントラクトの書き方
スマートコントラクトでは、正確な精度を確保することが非常に重要です。 Rust 言語にも整数演算の結果の精度が失われるという問題がありますが、次のような保護措置を講じることで精度を向上させ、満足のいく結果を得ることができます。
3.1 操作の操作順序を調整する
整数の除算よりも整数の乗算を優先します。
3.2 整数の大きさの桁を上げる
整数はより大きな桁数を使用し、より大きな分子を作成します。
たとえば、NEAR トークンの場合、上記のように N = 10 と定義すると、NEAR 値 5.123 を表現する必要がある場合、実際の演算で使用される整数値は 5.123* 10^10 = として表現されることを意味します。 51_230_000_000 。この値は後続の整数演算に引き続き関与するため、演算の精度が向上します。
3.3 累積演算精度の損失
避けられない整数計算精度の問題については、プロジェクト当事者は、計算精度の累積損失を記録することを検討できます。

次のように fn distribution(amount: u128, offset: u128) -> u128 を使用して USER_NUM ユーザーにトークンを配布するシナリオを想定します。
このテスト ケースでは、システムは毎回 10 個のトークンを 3 人のユーザーに配布します。ただし、整数計算の精度により、最初のラウンドで per_user_share を計算すると、得られる整数計算結果は 10 / 3 = 3 になります。つまり、最初の配布ラウンドのユーザーは平均して 3 つのトークンを受け取り、合計で 3 つのトークンを受け取ります。 9 個のトークンが配布されます。
この時点で、ユーザーに配布されていないトークンがシステム内にまだ 1 つあることがわかります。このため、残ったトークンをシステムグローバル変数offsetに一時的に保存することが考えられます。次回、distribute システムコールがユーザーにトークンを配布するのを待って、この値が取り出され、今回のラウンドで配布されたトークンの量と合わせてユーザーに配布されます。
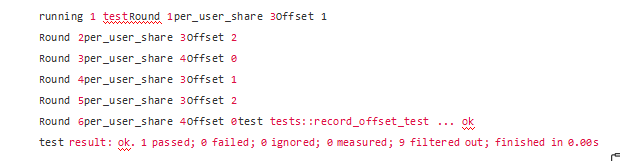
シミュレートされたトークン配布プロセスは次のとおりです。
システムが第 3 ラウンドでトークンの配布を開始すると、システムの累積オフセット値が 2 に達しており、この値が今回のラウンドで配布される 10 個のトークンと追加されて再度ユーザーに配布されることがわかります。 。 (この計算では、per_user_share = token_to_distribute / USER_NUM = 12 / 3 = 4 という精度の損失はありません。)
全体として、最初の 3 ラウンドで、システムは合計 30 個のトークンを発行しました。各ユーザーは各ラウンドで 3 個、3 個、4 個のトークンを獲得し、この時点で合計 30 個のトークンを獲得し、ボーナスを完全に配布するというシステムの目標を達成しました。
3.4 Rust Crate ライブラリrust-10進数の使用
この Rust ライブラリは、効率的な精度の計算と丸め誤差のない小数財務計算に適しています。
3.5 丸めメカニズムを考慮する





