tiêu đề phụ

1. Độ chính xác của số học dấu phẩy động

Hiện tại, các ngôn ngữ máy tính chính thống hầu hết tuân theo tiêu chuẩn IEEE 754 để biểu diễn các số dấu phẩy động và ngôn ngữ Rust cũng không ngoại lệ. Sau đây là mô tả về kiểu dấu chấm động chính xác kép f64 bằng ngôn ngữ Rust và dạng lưu trữ dữ liệu nhị phân trong máy tính:

hình ảnh

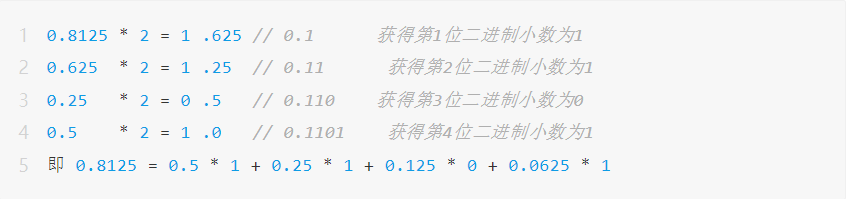
Các số dấu phẩy động được thể hiện bằng ký hiệu khoa học với cơ số là 2. Ví dụ: số nhị phân 0,1101 với số lượng chữ số hạn chế có thể được sử dụng để biểu thị số thập phân 0,8125. Phương pháp chuyển đổi cụ thể như sau:

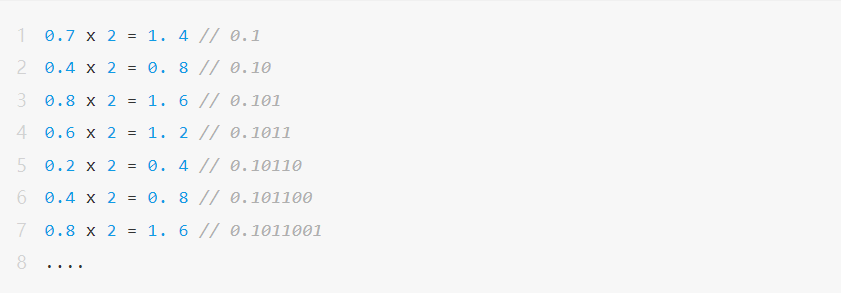
Tuy nhiên, đối với số thập phân 0,7 khác, sẽ có các vấn đề sau trong quá trình chuyển đổi thực sự nó thành số dấu phẩy động:

Tức là số thập phân 0,7 sẽ được biểu diễn thành 0,101100110011001100.....(vòng lặp vô hạn), không thể biểu diễn chính xác bằng số dấu phẩy động có độ dài bit hữu hạn và xảy ra hiện tượng "làm tròn (Làm tròn)" .

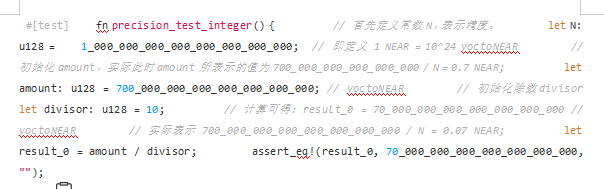
Giả sử rằng trên chuỗi công khai NEAR, 0,7 mã thông báo NEAR cần được phân phối cho mười người dùng, số lượng mã thông báo NEAR cụ thể được phân phối cho mỗi người dùng sẽ được tính toán và lưu trong biến result_0.

Đầu ra của việc thực hiện trường hợp thử nghiệm này như sau:

Có thể thấy rằng trong các phép toán dấu phẩy động ở trên, giá trị của số tiền không đại diện chính xác cho 0,7, mà là một giá trị rất gần đúng của 0,69999999999999995559. Ngoài ra, đối với một phép toán chia đơn lẻ chẳng hạn như số tiền/số chia, kết quả phép toán cũng sẽ trở thành một giá trị không chính xác 0,069999999999999999, chứ không phải 0,07 như mong đợi. Điều này cho thấy sự không chắc chắn của số học dấu phẩy động.

1. Về vấn đề này, chúng tôi phải xem xét sử dụng các loại phương pháp biểu diễn số khác trong hợp đồng thông minh, chẳng hạn như số điểm cố định.

2. Theo vị trí cố định của dấu thập phân của các số có dấu phẩy cố định, có hai loại số có dấu phẩy cố định: số nguyên có dấu phẩy cố định (thuần túy) và số thập phân có dấu phẩy cố định (thuần túy).

Nếu dấu thập phân được cố định sau chữ số nhỏ nhất của số đó thì nó được gọi là số nguyên có dấu phẩy cố định

Trong văn bản hợp đồng thông minh thực tế, một phân số có mẫu số cố định thường được sử dụng để biểu thị một giá trị nhất định, chẳng hạn như phân số ' x/N ', trong đó ' N ' là hằng số và ' x ' có thể thay đổi.

Nếu giá trị của "N" là "1.000.000.000.000.000.000", nghĩa là: ' 10^18 ', thì số thập phân có thể được biểu thị dưới dạng số nguyên, như sau:

Trong Giao thức NEAR, giá trị phổ biến của N là ' 10^24 ', nghĩa là 10^24 yoctoNEAR tương đương với 1 mã thông báo NEAR.

Dựa vào đây, chúng ta có thể sửa unit test trong phần này để tính toán như sau:

Bằng cách này, có thể thu được kết quả tính toán thống kê số: 0,7 GẦN / 10 = 0,07 GẦN

2. Vấn đề độ chính xác của phép tính số nguyên Rust

Từ mô tả trong Phần 1 ở trên, có thể thấy rằng việc sử dụng các phép toán số nguyên có thể giải quyết vấn đề mất độ chính xác trong các phép toán dấu phẩy động trong các tình huống phép toán nhất định.

Tuy nhiên, điều này không có nghĩa là kết quả tính toán sử dụng số nguyên là hoàn toàn chính xác và đáng tin cậy. Phần này mô tả một số lý do ảnh hưởng đến độ chính xác của phép tính số nguyên.

2.1 Trình tự thao tác

Đối với phép nhân và phép chia có cùng mức độ ưu tiên số học, việc thay đổi dãy số có thể ảnh hưởng trực tiếp đến kết quả tính toán, dẫn đến vấn đề độ chính xác của phép tính số nguyên.

Ví dụ, các hoạt động sau đây tồn tại:

Kết quả thực hiện unit test như sau:

Chúng ta có thể thấy rằng result_0 = a * c / b và result_1 = (a / b) * c mặc dù công thức tính toán của chúng giống nhau nhưng kết quả lại khác nhau.

Lý do cụ thể của việc phân tích là: Đối với phép chia số nguyên, độ chính xác nhỏ hơn số chia sẽ bị loại bỏ. Do đó, trong quá trình tính kết quả_1, kết quả được tính đầu tiên (a / b) trước sẽ mất độ chính xác của phép tính và trở thành 0; trong khi khi tính kết quả_0, kết quả của a * c sẽ được tính trước 20_0000, kết quả này sẽ lớn hơn hơn số chia b, do đó tránh được vấn đề mất độ chính xác và có thể thu được kết quả tính toán chính xác.

2.2 Bậc độ lớn quá nhỏ

Kết quả cụ thể của unit test này như sau:

Có thể thấy rằng kết quả tính toán result_0 và result_1 tương đương của quá trình tính toán không giống nhau và result_1 = 13 gần với giá trị tính toán dự kiến ​​thực tế hơn: 13.3333....

3. Cách viết hợp đồng thông minh Rust theo số

Đảm bảo độ chính xác chính xác là rất quan trọng trong hợp đồng thông minh. Mặc dù ngôn ngữ Rust cũng có vấn đề về việc mất độ chính xác trong kết quả của các phép toán số nguyên, nhưng chúng ta có thể thực hiện các biện pháp bảo vệ sau để cải thiện độ chính xác và đạt được kết quả khả quan.

• 3.1 Điều chỉnh thứ tự thao tác của thao tác

Thích phép nhân số nguyên hơn phép chia số nguyên.

3.2 Tăng bậc các số nguyên

Các số nguyên sử dụng các bậc độ lớn lớn hơn, tạo ra các phân tử lớn hơn.

Ví dụ: đối với mã thông báo NEAR, nếu bạn xác định N = 10 như mô tả ở trên, điều đó có nghĩa là: nếu bạn cần biểu thị giá trị NEAR là 5,123, thì giá trị số nguyên được sử dụng trong hoạt động thực tế sẽ được biểu thị là 5,123* 10^10 = 51_230_000_000 . Giá trị này tiếp tục tham gia vào các hoạt động số nguyên tiếp theo, có thể cải thiện độ chính xác của hoạt động.

3.3 Mất độ chính xác hoạt động tích lũy

Đối với các vấn đề về độ chính xác của phép tính số nguyên không thể tránh khỏi, bên dự án có thể xem xét ghi lại sự mất mát tích lũy của độ chính xác của phép tính.

Giả sử kịch bản sử dụng fn phân phối(số tiền: u128, bù: u128) -> u128 để phân phối mã thông báo cho USER_NUM người dùng như sau.

Trong trường hợp thử nghiệm này, hệ thống sẽ phân phối 10 Token cho 3 người dùng mỗi lần. Tuy nhiên, do độ chính xác của các phép tính số nguyên, khi tính toán per_user_share trong vòng đầu tiên, kết quả tính toán số nguyên thu được là 10/3 = 3, tức là người dùng trong vòng phân phối đầu tiên sẽ nhận được trung bình 3 mã thông báo và tổng cộng trong số 9 mã thông báo sẽ được phân phối.

Tại thời điểm này, có thể thấy rằng vẫn còn một mã thông báo trong hệ thống chưa được phân phối cho người dùng. Vì lý do này, có thể xem xét tạm thời lưu mã thông báo còn lại trong phần bù biến toàn cục của hệ thống. Đợi lần sau hệ thống gọi phân phối để phân phối token cho người dùng, giá trị này sẽ được lấy ra và cố gắng phân phối cho người dùng cùng với lượng token đã phân phối trong đợt này.

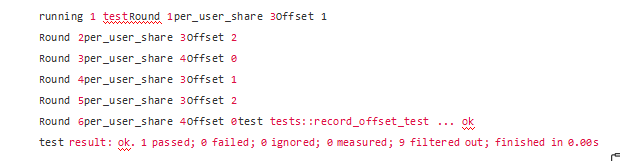
Quá trình phân phối mã thông báo mô phỏng như sau:

Có thể thấy rằng khi hệ thống bắt đầu phân phối mã thông báo trong vòng thứ ba, giá trị bù tích lũy của hệ thống đã đạt đến 2 và giá trị này sẽ được cộng lại cùng với 10 mã thông báo sẽ được phân phối lại trong vòng này và phân phối cho người dùng . (Sẽ không mất độ chính xác trong phép tính này per_user_share = token_to_distribute / USER_NUM = 12/3 = 4.)

Nhìn chung, trong 3 đợt đầu tiên, hệ thống đã phát hành tổng cộng 30 Token. Mỗi người dùng đã nhận được 3, 3 và 4 mã thông báo trong mỗi vòng, tại thời điểm này, người dùng cũng đã nhận được tổng cộng 30 mã thông báo, điều này đã đạt được mục tiêu của hệ thống là phân phối đầy đủ tiền thưởng.

3.4 Sử dụng thư viện Rust Crate Rust-decimal

Thư viện Rust này phù hợp với các tính toán tài chính phân số yêu cầu tính toán chính xác hiệu quả và không có lỗi làm tròn.

3.5 Xem xét cơ chế làm tròn