Tiêu đề gốc: "Hàng khô | Chữ ký Schnorr có thể cải thiện Bitcoin như thế nào", tác giả Stepan

Trong khi đọc bài báo MuSig của Blockstream, tôi cứ tưởng tượng điều này có ý nghĩa gì đối với tôi với tư cách là một người dùng Bitcoin. Tôi đã tìm thấy một số tính năng của chữ ký Schnorr thực sự thú vị và tiện lợi, và một số tính năng khá khó chịu. Trong bài viết này, tôi hy vọng sẽ chia sẻ suy nghĩ của tôi với bạn. Nhưng trước tiên, hãy tóm tắt nhanh.

Thuật toán chữ ký đường cong elip

Hệ thống sở hữu Bitcoin hiện tại sử dụng ECDSA (Thuật toán chữ ký đường cong Elliptic). Khi ký một tin nhắn m, trước tiên chúng ta băm tin nhắn để nhận giá trị băm, tức là z = hash(m) . Chúng ta cũng cần một số ngẫu nhiên (hoặc ít nhất là có vẻ ngẫu nhiên) k. Ở đây, chúng tôi không muốn tin tưởng trình tạo số ngẫu nhiên (có quá nhiều lỗi và lỗi liên quan đến trình tạo số ngẫu nhiên không đạt tiêu chuẩn), vì vậy chúng tôi thường sử dụng RFC6979, dựa trên một giá trị bí mật mà chúng tôi biết và chúng tôi muốn ký thông báo, tính toán một k xác định.

Sử dụng khóa riêng pk , chúng ta có thể tạo chữ ký cho thông báo m bao gồm hai số: r (tọa độ x của một điểm ngẫu nhiên R = k * G) và s = ​​(z + r*pk)/k.

Mô tả hình ảnh

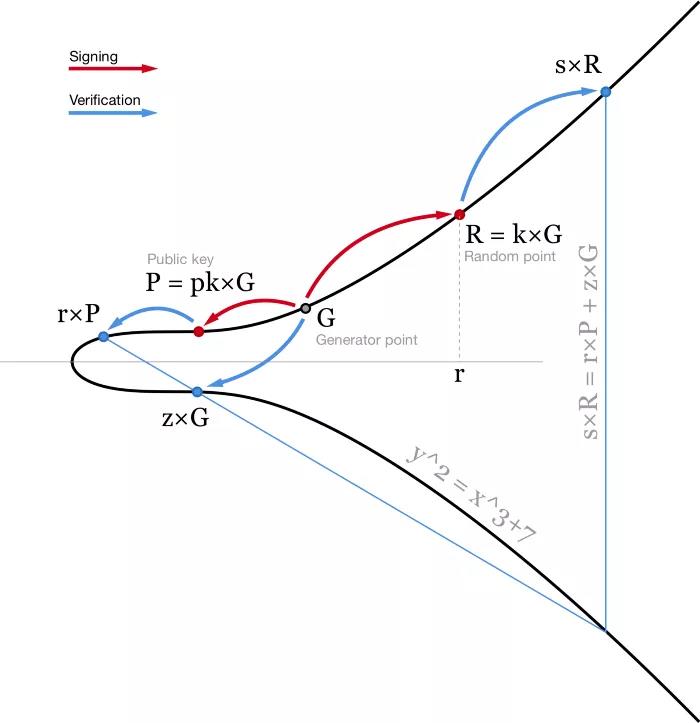
- Sơ đồ thuật toán ECDSA. Đối với mục đích minh họa, các đường cong elip hoạt động trên trường số thực -

Thuật toán này rất phổ biến và rất dễ sử dụng. Nhưng vẫn còn chỗ để cải thiện. Đầu tiên, việc xác minh chữ ký bao gồm phép chia (1/s) và phép nhân hai dấu chấm, và các thao tác này đòi hỏi rất nhiều tính toán. Trong mạng Bitcoin, mọi nút phải xác minh mọi giao dịch, vì vậy khi bạn gửi một giao dịch trong mạng, hàng nghìn nút trong toàn bộ mạng phải xác minh chữ ký của bạn. Vì vậy, ngay cả khi quá trình ký trở nên tốn kém hơn, nó vẫn rất có lợi để giúp xác minh chữ ký dễ dàng hơn.

chữ ký Schnorr

chữ ký Schnorr

Mô tả hình ảnh

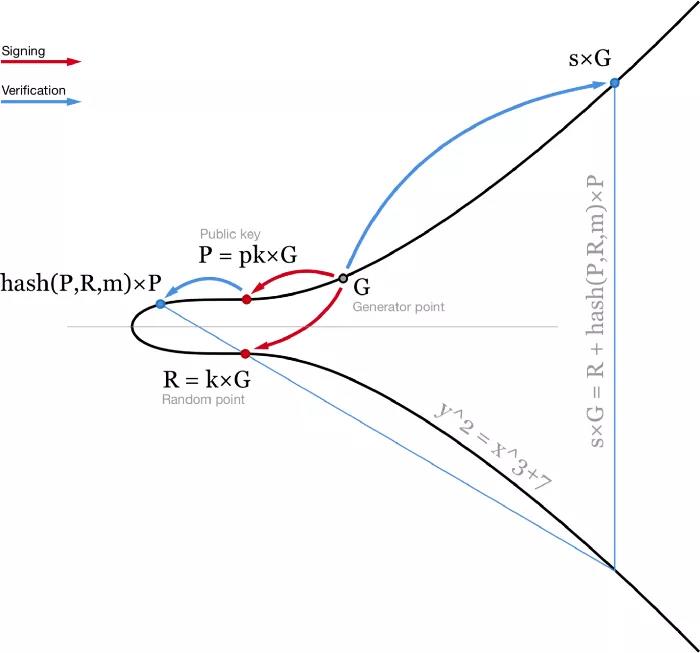
- Chữ ký Schnorr đồ họa và xác minh -

Phương trình này là tuyến tính, vì vậy có thể cộng và trừ nhiều phương trình trong khi dấu đẳng thức vẫn giữ nguyên. Điều này đưa chúng ta đến một số thuộc tính tốt đẹp của chữ ký Schnorr.

1. Xác minh hàng loạt

Khi xác thực một khối trên chuỗi khối, chúng tôi cần xác minh rằng chữ ký của tất cả các giao dịch trong khối là hợp lệ. Nếu một trong số chúng không hợp lệ, thì cái nào không quan trọng - chúng ta phải từ chối toàn bộ khối.

Mỗi chữ ký của ECDSA phải được xác minh cụ thể, nghĩa là nếu một khối chứa 1000 chữ ký, thì chúng ta cần tính toán 1000 phép chia và 2000 phép nhân điểm, tổng cộng khoảng 3000 phép tính nặng.

Nhưng với chữ ký Schnorr, chúng ta có thể cộng tất cả các phương trình xác minh chữ ký và tiết kiệm một số tính toán. Trong một khối 1000 giao dịch, chúng tôi có thể xác minh:

(s1+s2+…+s1000) × G=(R1+…+R1000)+(hash(P1,R1,m1)×P1+ hash(P2,R2,m2)×P2+…+hash(P1000,R1000,m1000)×P1000)

Mô tả hình ảnh

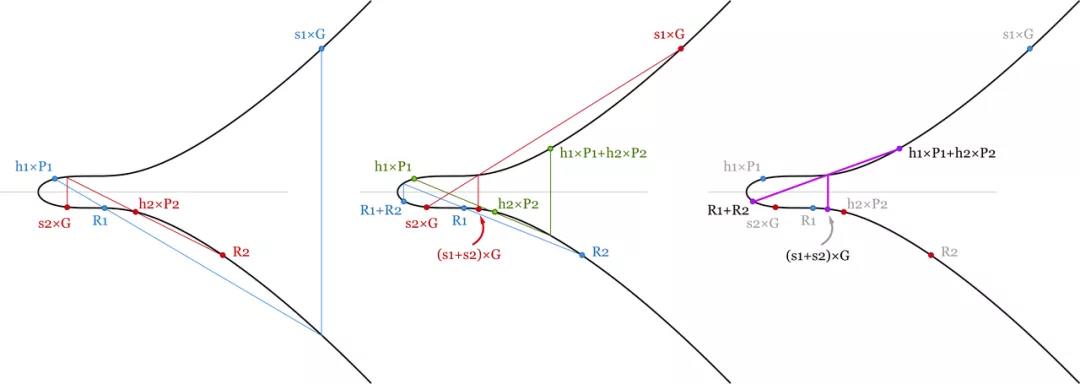
- Xác minh hàng loạt hai chữ ký. Bởi vì phương trình xác minh là cộng tuyến tính, miễn là tất cả các chữ ký đều hợp lệ, tổng của các phương trình này cũng phải được thiết lập. Chúng tôi tiết kiệm một số tính toán vì phép cộng vô hướng và điểm dễ tính toán hơn nhiều so với phép nhân điểm. -

2. Tạo khóa

Chúng tôi muốn giữ an toàn cho bitcoin của mình, vì vậy chúng tôi có thể muốn kiểm soát chúng bằng ít nhất hai khóa riêng tư khác nhau. Một cái được sử dụng trên máy tính xách tay hoặc điện thoại di động (ví trực tuyến, ví nóng) và cái còn lại được giữ trong ví phần cứng/ví lạnh. Ngay cả khi một trong số chúng bị rò rỉ, chúng tôi vẫn kiểm soát bitcoin của mình.

Hiện tại, cách để triển khai ví như vậy là thông qua tập lệnh đa chữ ký 2-2. Nghĩa là, một giao dịch cần có hai chữ ký độc lập.

Với chữ ký Schnorr, chúng ta có thể lấy một cặp khóa (pk1,pk2) và tạo chữ ký chung bằng cách sử dụng khóa chung P = P1 + P2 = pk1 * G + pk2 * G. Khi tạo chữ ký, chúng ta cần tạo một số ngẫu nhiên (k1, k2) trên hai thiết bị và tạo hai điểm ngẫu nhiên Ri = ki * G và thêm hàm băm (P, R1 + R2, m ), bạn có thể nhận được s1 và s2 (vì si = ki + hash(P, R, m)* pki ). Cuối cùng, cộng tất cả chúng lại để có chữ ký (R, s) = (R1+R2, s1+s2), là chữ ký dùng chung của chúng ta, chữ ký này có thể được xác minh bằng khóa công khai dùng chung. Không ai khác có thể biết đó có phải là chữ ký tổng hợp hay không, nó trông giống như chữ ký Schnorr bình thường.

Tuy nhiên, có ba vấn đề với cách tiếp cận này.

Vấn đề đầu tiên là trên giao diện người dùng. Để bắt đầu một giao dịch, chúng ta cần bắt đầu nhiều vòng tương tác trên hai thiết bị - để tính R chung và để ký. Trong trường hợp có hai khóa riêng, chúng tôi chỉ cần truy cập ví lạnh một lần: chúng tôi có thể chuẩn bị giao dịch được ký trong ví nóng, chọn k1 và tạo R1 = k1 * G, sau đó đặt giao dịch được ký cùng nhau với những dữ liệu này Chuyển vào ví lạnh và ký tên. Vì đã có R1 nên giao dịch chữ ký có thể được hoàn thành chỉ trong một vòng trong ví lạnh. Từ ví lạnh, chúng tôi nhận được R2 và s2 và gửi lại cho ví nóng. Ví nóng sử dụng giao dịch chữ ký (k1, R1) đã nói ở trên và tổng của hai chữ ký có thể phát giao dịch ra thế giới bên ngoài.

Trải nghiệm này không khác gì những gì chúng ta có thể làm bây giờ và mỗi khi bạn thêm một khóa riêng tư bổ sung, vấn đề sẽ trở nên phức tạp hơn. Giả sử bạn có một khối tài sản được kiểm soát chung bởi 10 khóa riêng tư và 10 khóa riêng tư được lưu trữ ở những nơi khác nhau trên thế giới, thật phiền phức cho bạn khi gửi giao dịch vào thời điểm này! Trong thuật toán ECDSA hiện tại, bạn chỉ cần truy cập từng thiết bị một lần, nhưng nếu bạn sử dụng tập hợp khóa của Schnorr, bạn cần truy cập hai lần để lấy tất cả Ri và ký. Trong trường hợp này, thay vì tổng hợp, có thể tốt hơn là ký với từng khóa riêng tư - để chỉ cần một vòng tương tác.

Sau khi bài viết kết thúc, tôi nhận được phản hồi từ Manu Drijvers: Trong sơ đồ đa chữ ký được chứng minh là an toàn, bạn cần 3 vòng tương tác:

• Chọn một số ngẫu nhiên ki và điểm ngẫu nhiên tương ứng Ri = ki \G, sau đó cho từng thiết bị biết giá trị băm của Ri ti=hash(Ri), sau đó mỗi thiết bị có thể đảm bảo rằng bạn không biết ý tưởng thay đổi số ngẫu nhiên của người khác*

• dấu hiệu

• dấu hiệu

Vấn đề thứ hai là cuộc tấn công khóa Rogue đã biết. Bài viết giải thích nó rất tốt, vì vậy tôi sẽ không đi vào chi tiết. Điều đó có thể có nghĩa là nếu một trong các thiết bị của bạn bị tấn công (ví dụ: ví nóng của bạn bị xâm nhập) và giả vờ rằng khóa chung của bạn là (P1 - P2), thì bạn chỉ có thể kiểm soát khóa riêng tư được chia sẻ của hai khóa riêng tư đó. chìa khóa pk1 quỹ. Một giải pháp đơn giản là yêu cầu khóa riêng để ký khóa chung tương ứng khi thiết lập thiết bị.

Có một vấn đề lớn thứ ba. Bạn không thể ký với k xác định. Nếu bạn sử dụng k xác định, tin tặc có thể lấy khóa riêng của bạn chỉ bằng một cuộc tấn công đơn giản. Đây là cuộc tấn công: Một số hacker xâm nhập vào máy tính xách tay của bạn và kiểm soát hoàn toàn một trong các khóa riêng (giả sử pk1). Chúng tôi cảm thấy tiền vẫn an toàn, bởi vì việc sử dụng bitcoin của chúng tôi yêu cầu chữ ký tổng hợp của pk1 và pk2. Vì vậy, chúng tôi bắt đầu một giao dịch như bình thường, chuẩn bị một giao dịch được ký và R1, gửi nó đến ví phần cứng của chúng tôi và sau khi ví phần cứng ký, hãy gửi (R2, s2) trở lại ví nóng... Sau đó, ví nóng ví đã xảy ra lỗi, Không thể hoàn tất việc ký và phát. Vì vậy, chúng tôi thử lại, nhưng lần này máy tính bị tấn công sử dụng một số ngẫu nhiên khác - R1' . Chúng tôi đã ký giao dịch tương tự trong ví phần cứng của mình và gửi (R2, s2') trở lại máy tính bị tấn công. Lần này, không còn nữa - tất cả bitcoin của chúng tôi đã biến mất.

Trong cuộc tấn công này, tin tặc đã lấy được hai chữ ký hợp lệ của cùng một giao dịch: (R1, s1, R2, s2) và (R1', s1', R2, s2'). R2 này giống nhau, nhưng R = R1 + R2 và R' = R1' + R2 thì khác. Điều này có nghĩa là tin tặc có thể tính toán khóa riêng thứ hai của chúng ta: s2-s2'=(hash(P,R1+R2,m)-hash(P,R1'+R2,m))⋅pk2 hoặc pk2 =(s2-s2 ')/(băm(P,R1+R2,m)-hash(P,R1'+R2,m)). Tôi thấy đây là phần bất tiện nhất trong quá trình tổng hợp khóa - chúng tôi phải sử dụng một trình tạo số ngẫu nhiên tốt mỗi lần để tổng hợp một cách an toàn.

3. Musig

MuSig đã giải quyết được một trong những vấn đề - các cuộc tấn công bằng phím lừa đảo sẽ không còn hiệu quả nữa. Mục tiêu ở đây là tổng hợp chữ ký và khóa công khai từ nhiều bên/nhiều cài đặt mà không yêu cầu bạn chứng minh rằng bạn có khóa riêng tư tương ứng với các khóa chung đó.

Chữ ký tổng hợp tương ứng với khóa chung tổng hợp. Nhưng trong MuSig, thay vì thêm trực tiếp các khóa công khai của tất cả những người đồng ký tên, chúng tôi nhân chúng với một số tham số để khóa công khai tổng hợp P = hash(L,P1)×P1 + ... + hash(L,Pn )×Pn. Ở đây, L = hash(P1,...,Pn) - số công khai này dựa trên tất cả các khóa công khai. Thuộc tính phi tuyến của L ngăn chặn kẻ tấn công xây dựng một khóa công khai đặc biệt để khởi động một cuộc tấn công. Ngay cả khi kẻ tấn công biết hàm băm(L,Patk)×Patk của anh ta phải là bao nhiêu, thì anh ta cũng không thể suy ra Patk từ nó—điều đó cũng giống như việc bạn muốn suy ra khóa riêng tư từ khóa chung.

Các quy trình khác của việc xây dựng chữ ký rất giống với quy trình được mô tả ở trên. Khi tạo chữ ký, mỗi người đồng ký chọn một số ki ngẫu nhiên và chia sẻ Ri = ki * G với những người khác. Sau đó, họ cộng tất cả các điểm ngẫu nhiên để có R=R1+…+Rn , rồi tạo chữ ký si = ki + hash(P,R,m) ⋅ hash(L,Pi) ⋅ pki . Do đó, chữ ký tổng hợp là (R, s)=(R1+…+Rn, s1+…+sn) và cách xác minh chữ ký vẫn giống như trước đây: s×G = R + hash(P,R,m )×P .

4. Cây Merkle đa chữ ký

Bạn cũng có thể nhận thấy rằng MuSig và tổng hợp khóa yêu cầu *tất cả người ký phải ký giao dịch*. Nhưng nếu những gì bạn muốn làm là một tập lệnh đa chữ ký 2-3 thì sao? Chúng tôi có thể sử dụng tổng hợp chữ ký vào thời điểm này hay chúng tôi phải sử dụng OP_CHECKMULTISIG thông thường và ký riêng? (Ghi chú của người dịch: OP_CHECKMULTISIG là mã hoạt động của Bitcoin để xác minh tập lệnh đa chữ ký đường cong elip)

Hãy để tôi bắt đầu với câu trả lời, có, nhưng thỏa thuận sẽ hơi khác một chút. Chúng ta có thể phát triển một opcode tương tự như OP_CHECKMULTISIG, ngoại trừ việc nó kiểm tra xem chữ ký tổng hợp có tương ứng với một phần tử trên cây Merkle khóa công khai hay không.

Ví dụ: nếu chúng ta muốn sử dụng các khóa công khai P1, P2 và P3 để tạo tập lệnh đa chữ ký 2-3, chúng ta cần sử dụng tất cả các cặp khóa công khai này (P1, P2), (P2, P3), (P1 , P3) để xây dựng cây Merkle và xuất bản gốc của cây Merkle trong tập lệnh khóa.

chữ

Nhưng với cây khóa công khai Merkle, chúng ta không bị giới hạn ở mn tập lệnh đa chữ ký. Chúng ta có thể tạo một cây bằng cách sử dụng bất kỳ tổ hợp khóa công khai nào. Ví dụ: nếu chúng tôi có máy tính xách tay, điện thoại, ví phần cứng và bộ ghi nhớ, chúng tôi có thể xây dựng cây Merkle cho phép chúng tôi sử dụng máy tính xách tay + ví phần cứng, điện thoại + ví phần cứng hoặc ghi nhớ riêng các từ để sử dụng Bitcoin . Đây là điều mà OP_CHECKMULTISIG hiện tại không thể làm được - trừ khi bạn sử dụng điều khiển luồng kiểu "NẾU - Khác" để xây dựng các tập lệnh phức tạp hơn.

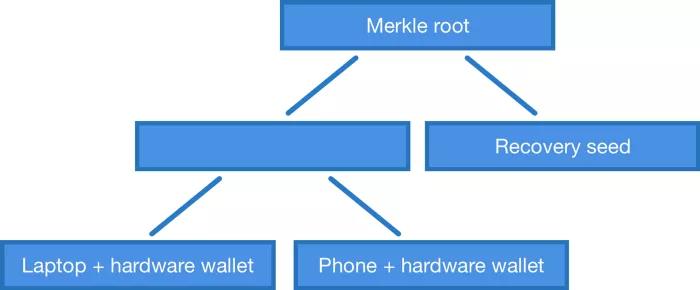
Tóm lại là

Chữ ký Schnorr rất tuyệt, chúng giải quyết một số chi phí tính toán trong xác minh khối và cũng cung cấp cho chúng tôi tổng hợp khóa. Cái sau hơi bất tiện khi sử dụng, nhưng chúng tôi không bắt buộc mọi người sử dụng nó - dù sao thì chúng tôi vẫn có thể sử dụng các sơ đồ đa chữ ký thông thường, sử dụng các chữ ký riêng lẻ, không tổng hợp.

Tôi nóng lòng muốn sử dụng chữ ký Schnorr, hy vọng giao thức Bitcoin sẽ sớm kết hợp chúng.

(qua)

(qua)