보조 제목
1. 부동 소수점 산술의 정밀도
현재 주류 컴퓨터 언어는 대부분 부동 소수점 숫자를 나타내는 IEEE 754 표준을 따르고 있으며 Rust 언어도 예외는 아닙니다. 다음은 Rust 언어의 배정밀도 부동 소수점 유형 f64와 컴퓨터의 이진 데이터 저장 형식에 대한 설명입니다.
그림
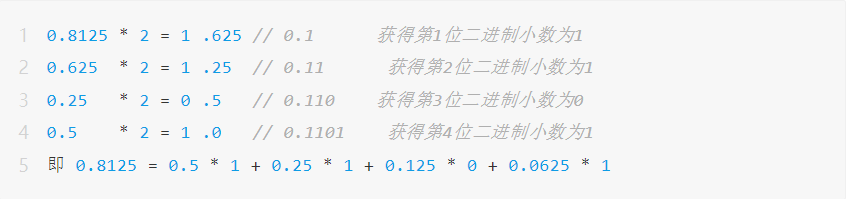
부동 소수점 숫자는 밑이 2인 과학적 표기법으로 표현됩니다. 예를 들어, 자릿수가 제한된 이진수 0.1101은 십진수 0.8125를 나타내는 데 사용할 수 있습니다.구체적인 변환 방법은 다음과 같습니다.
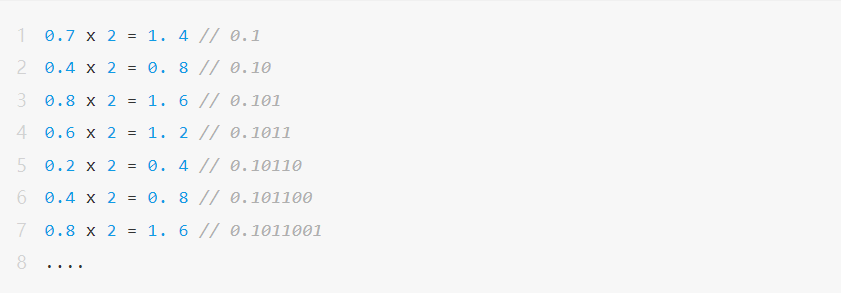
그러나 또 다른 십진수 0.7의 경우 이를 실제로 부동소수점으로 변환하는 과정에서 다음과 같은 문제가 발생하게 됩니다.
즉, 십진수 0.7은 0.101100110011001100.....(무한 루프)로 표현될 것이고, 이는 비트 길이가 유한한 부동소수점수로 정확하게 표현할 수 없고, "반올림(Rounding)" 현상이 발생한다. .

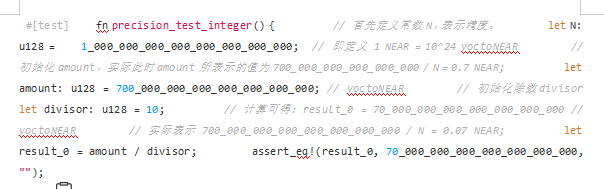
NEAR 퍼블릭 체인에서 0.7개의 NEAR 토큰을 10명의 사용자에게 배포해야 한다고 가정하면 각 사용자에게 배포되는 NEAR 토큰의 특정 수를 계산하여 result_0 변수에 저장합니다.

이 테스트 사례를 실행한 결과는 다음과 같습니다.
위의 부동 소수점 계산에서 amount의 값이 정확히 0.7을 나타내는 것이 아니라 0.69999999999999995559라는 매우 근사한 값임을 알 수 있습니다. 또한 amount/divisor와 같은 단일 나눗셈 연산의 경우 연산 결과도 예상한 0.07이 아니라 부정확한 0.069999999999999999가 됩니다. 이것은 부동 소수점 산술의 불확실성을 보여줍니다.
이와 관련하여 스마트 계약에서 고정 소수점 숫자와 같은 다른 유형의 수치 표현 방법을 사용하는 것을 고려해야 합니다.
고정 소수점 숫자의 소수점 고정 위치에 따라 고정 소수점 숫자에는 고정 소수점(순수) 정수와 고정 소수점(순수) 소수의 두 가지 유형이 있습니다.
숫자의 가장 낮은 자리 뒤에 소수점이 고정되어 있으면 고정 소수점 정수라고 합니다.
실제 스마트 컨트랙트 작성에서 분모가 고정된 분수는 일반적으로 분수 'x/N'과 같이 특정 값을 나타내는 데 사용되며 여기서 'N'은 상수이고 'x'는 달라질 수 있습니다.

"N"의 값이 "1,000,000,000,000,000,000", 즉 ' 10^18 '이면 소수점은 다음과 같이 정수로 표현할 수 있습니다.
NEAR 프로토콜에서 N의 공통 값은 '10^24'입니다. 즉, 10^24 yoctoNEAR는 1 NEAR 토큰과 같습니다.
이를 바탕으로 이 섹션의 단위 테스트를 수정하여 다음과 같이 계산할 수 있습니다.

이러한 방식으로 수치 계리 계산 결과를 얻을 수 있습니다. 0.7 NEAR / 10 = 0.07 NEAR
2. Rust 정수 계산 정확도 문제
위 섹션 1의 설명에서 정수 연산을 사용하면 특정 연산 시나리오에서 부동 소수점 연산의 정밀도 손실 문제를 해결할 수 있음을 알 수 있습니다.
그러나 이것이 정수를 사용한 계산 결과가 완전히 정확하고 신뢰할 수 있음을 의미하지는 않습니다. 이 섹션에서는 정수 계산의 정밀도에 영향을 미치는 몇 가지 이유에 대해 설명합니다.
2.1 동작순서
산술 우선순위가 같은 곱셈과 나눗셈의 경우 수열이 바뀌면 계산 결과에 직접적인 영향을 미쳐 정수 계산 정확도에 문제가 생길 수 있습니다.

예를 들어 다음 작업이 있습니다.

단위 테스트 실행 결과는 다음과 같습니다.
result_0 = a * c / b와 result_1 = (a / b) * c는 계산식은 같으나 결과는 다르다는 것을 알 수 있다.
분석의 구체적인 이유는 다음과 같습니다. 정수 나누기의 경우 제수보다 작은 정밀도는 버려집니다. 따라서 result_1을 계산하는 과정에서 먼저 계산된 (a/b)가 먼저 계산 정밀도를 잃어 0이 되고, result_0을 계산할 때 a * c의 결과가 먼저 20_0000으로 계산되어 계산 정밀도보다 크게 된다. 약수 b이므로 정밀도 손실 문제를 피하고 올바른 계산 결과를 얻을 수 있습니다.

2.2 크기가 너무 작음

이 단위 테스트의 구체적인 결과는 다음과 같습니다.
계산 프로세스의 등가 result_0 및 result_1 계산 결과가 동일하지 않으며 result_1 = 13이 실제 예상 계산 값인 13.3333....에 더 가깝다는 것을 알 수 있습니다.
3. 수치계리 Rust 스마트 계약 작성 방법
정확한 정밀도를 보장하는 것은 스마트 계약에서 매우 중요합니다. Rust 언어도 정수 연산 결과의 정밀도 손실 문제가 있지만 정밀도를 개선하고 만족스러운 결과를 얻기 위해 다음과 같은 보호 조치를 취할 수 있습니다.
3.1 작업의 작업 순서 조정
정수 나누기보다 정수 곱셈을 선호합니다.
3.2 정수의 자릿수 증가
정수는 더 큰 자릿수를 사용하여 더 큰 분자를 생성합니다.
예를 들어 NEAR 토큰의 경우 위와 같이 N=10으로 정의하면 NEAR 값인 5.123을 표현해야 한다면 실제 연산에 사용되는 정수 값은 5.123* 10^10 = 51_230_000_000 . 이 값은 후속 정수 연산에 계속 참여하여 연산 정확도를 향상시킬 수 있습니다.
3.3 누적 연산 정밀도 손실
피할 수 없는 정수 계산 정밀도 문제의 경우 프로젝트 당사자는 계산 정밀도의 누적 손실을 기록하는 것을 고려할 수 있습니다.

다음과 같이 fn distribution(amount: u128, offset: u128) -> u128을 사용하여 USER_NUM 사용자에게 토큰을 배포하는 시나리오를 가정합니다.
이 테스트 사례에서 시스템은 매번 3명의 사용자에게 10개의 토큰을 배포합니다. 그러나 정수 계산의 정확성으로 인해 1차에서 per_user_share를 계산할 때 얻은 정수 계산 결과는 10 / 3 = 3입니다. 즉, 1차 분배 사용자는 평균 3개의 토큰을 받게 되며 총 총 9개의 토큰이 배포됩니다.
이 시점에서 사용자에게 배포되지 않은 토큰이 시스템에 아직 하나 있음을 알 수 있습니다. 이 때문에 남은 토큰을 시스템 전역 변수 offset에 임시 저장하는 것으로 볼 수 있다. 다음에 시스템 호출이 사용자에게 토큰을 분배하기 위해 분배할 때를 기다리면서 이 값을 빼서 이번 라운드에서 분배된 토큰의 양과 함께 사용자에게 분배하려고 시도합니다.
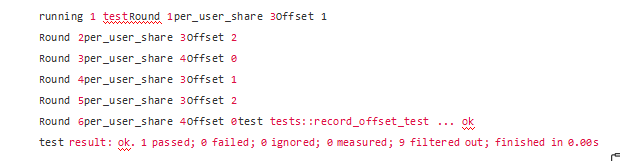
시뮬레이션된 토큰 배포 프로세스는 다음과 같습니다.
시스템이 3라운드에서 토큰 분배를 시작하면 시스템의 누적 오프셋 값이 2에 도달하고 이 값이 이번 라운드에서 다시 분배될 10개의 토큰과 함께 더해져 사용자에게 분배됨을 알 수 있습니다. . (이 계산에서 정밀도 손실은 없습니다. per_user_share = token_to_distribute / USER_NUM = 12 / 3 = 4.)
전체적으로 처음 3라운드에서 시스템은 총 30개의 토큰을 발행했습니다. 각 사용자는 각 라운드에서 3, 3, 4개의 토큰을 획득했으며, 이때 사용자는 총 30개의 토큰을 획득하여 보너스를 완전히 분배한다는 시스템의 목표를 달성했습니다.
3.4 Rust Crate 라이브러리 사용하기 rust-decimal
이 Rust 라이브러리는 효율적인 정밀 계산이 필요하고 반올림 오류가 없는 분수 재무 계산에 적합합니다.
3.5 반올림 메커니즘 고려





