Analysis of STARK algorithm
Part 0: Introduction
Part 1: Looking at STARK
Part 2: Useful "Tools"
Part 3: FRI
Part 4: STARK Polynomial IOPs
Part 5: A Rescue-Prime STARK
Part 6: Speed up the entire process
zk-SNARKs are generally general, meaning they can prove the integrity of any computation;
zk-SNARKs are non-interactive, meaning that the entire integrity proof consists of a single message;
The verification of zk-SNARKs is efficient, that is, the workload of the verifier is an order of magnitude less than that of simply rerunning the calculation (Translator's Note: Several orders of magnitude are also possible);
zk-SNARKs are zero-knowledge, meaning they don't reveal any information about computing secret inputs.
1. What are STARKs?
Recently, one of the most exciting developments in the field of cryptographic proof systems has been the development of STARKs. It comes after the booming blockchain industry. On the whole, proof systems seem to be tailor-made for them: blockchain networks are often composed of mutually distrusting parties who wish to use secret information to transact, or to update the collective state according to state evolution rules. Since participants are mutually distrustful, they need a way to verify the validity of transactions (or state updates) proposed by their peers.
Due to the following properties of zk-SNARKs, they are naturally capable of providing computational integrity guarantees in this environment:
While traditional zk-SNARKs rely on sophisticated cryptographic puzzles and assumptions, the only cryptographic component in the STARK proof system is a collision-resistant hash function. Therefore, under the idealized hash function model, the anti-quantum security of the proof system can be proved (in the literature, this idealization is called "quantum random oracle model" quantum random oracle model). This is in stark contrast to first-generation SNARKs, which used bilinear maps and were only provably secure under unfalsifiable assumptions.
Arithmeticization of STARKs is independent of cryptographically hard problems, so this domain can be specifically chosen to optimize performance. Therefore, STARKs make real fast proof (Prover) possible.
Traditional zk-SNARKs rely on a trusted setup ceremony to generate public parameters. After the ceremony, the random parameters used must be safely forgotten. The ceremony itself is not trustless, since if participants refuse or forget to delete this cryptographic "hazardous garbage", they retain the ability to forge proofs. In contrast, STARKs have no trusted setup and thus no cryptographic"hazardous waste".
Papers on FRI, STARK, DEEP-FRI, and the latest reliability analysis of FRI
A multi-part tutorial (Part 1/2/3) by Vitalik Buterin.
A series of blog posts from StarkWare (parts 1, 2, 3, 4, 5).
StarkWare's STARK@Home Webcast
StarkWare's STARK 101 Online Course
EthStark Documentation by StarkWare
In general, anything StarkWare puts out
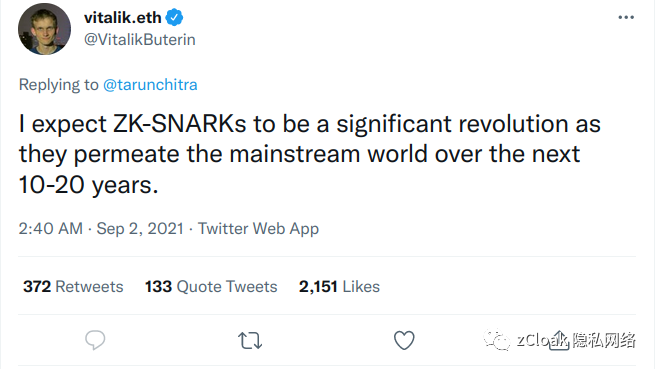
"I expect zk-SNARKs to penetrate the mainstream world in the next 10-20 years and lead a major revolution."—— "V God" 2021.9.2
zk-SNARKs have been around for a while, but STARK proof systems are a relatively new thing. It stands out for several reasons:
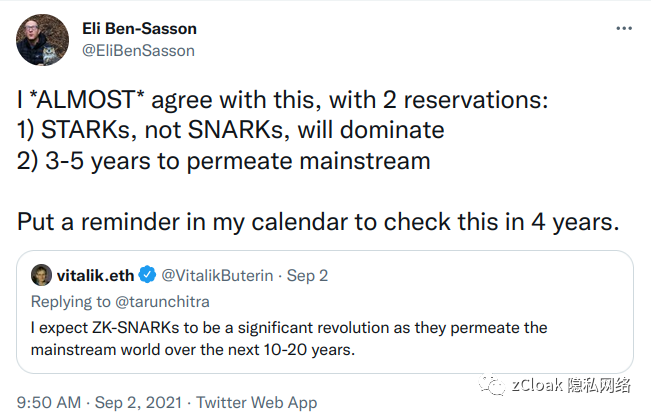
"I generally agree, with reservations on two points:
1) STARKs will dominate, not SNARKs
2) 3-5 years will penetrate the mainstream world
Put a reminder on my calendar to test those words 4 years from now. ——Eli Ben-Sasson 2021.9.2
In this tutorial, I'll explain how many of these parts work together. This literal explanation is supported by a Python implementation that proves and verifies simple computations based on the Rescue-Prime hash function. After reading or following this tutorial, you should be able to write your own zero-knowledge STARK provers and verifiers for computations of your choice
2. Why write this article?
It should be pointed out early that there are multiple sources of learning STARKs. Here is an incomplete list.
With so many learning resources, why am I writing another tutorial?
Finite fields and their extended fields
Polynomials over finite fields, including univariate and multivariate polynomials
hash function
hash function
Part 1: Looking at STARK describes the concept and workflow at a high level
Part 2: Useful "tools" introduces basic mathematical and cryptographic tools from which the proof system will be built
Part 3: FRI covers low-level testing, which is the cryptographic core of the proof system
Part 4: STARK Polynomial IOP(IOP,interactive oracle proof) explains information theory for generating abstract proof systems from arbitrary computational requirements
Part 5: A Rescue-Prime STARK puts these tools together to build a transparent zero-knowledge proof system for a simple computation
Part 6: Accelerate the entire process Introduce algorithms and technologies to make the entire process faster and effectively"S "(succinct, succinct) put in STARK
5. Acknowledgments
Existing tutorials are relatively shallow. These tutorials do a good job of explaining at a high level how these techniques work and convey an intuition as to why STARKs work. However, they do not describe a complete, deployable system. For example, none of the tutorials describe how to implement zero-knowledge, how to batch various low-level proofs, or how to determine the resulting security level. The EthSTARK documentation does provide a complete reference to answer most of these questions, but it is specific to a specific computation, does not cover zero knowledge, and does not give an accessible and intuitive explanation.
These papers are difficult to understand. Sadly, the incentives in scientific publishing are set up to make scientific papers difficult for lay readers. Therefore, tutorials like this article are needed to make these papers understandable to more people.
Information is outdated. Many of the techniques described in various tutorials have since been refined. For example, the EthSTARK documentation (the latest cited above) describes a DEEP interpolation technique in order to reduce the requirement for correct evaluation to polynomials of bounded degree. This technique is not mentioned in these sources because these sources predate the technique.
I prefer my own style. I disagree with a lot of symbols and names and I hope people use the correct ones. In particular, I like to focus on polynomials, as the most fundamental objects of proof systems. In contrast, all other sources describe the mechanism of proof systems in terms of operations on Reed-Solomon codewords.
This tutorial helped me understand STARK better. Writing this tutorial has helped me systematize my knowledge and find out where it is shallow or totally lacking.
3. Required background knowledge
This tutorial brushes up on some background knowledge as needed. However, it is recommended that all readers understand and study the following topics, as the introduction here may be too dense if they are not familiar with them.
4. Series Wizard
The authors would like to thank Bobbin Threadbare, Thorkil Værge, and Eli Ben-Sasson for their helpful feedback and comments, and the Nervos Foundation for their financial support. Email him: alan@nervos.org, or follow aszepieniec on twitter or Github.
Translator's Note: There are a large number of document links in the original text, which cannot be attached due to the limitation of the official account. Readers are requested to refer to the document links in the original text.
About zCloak Network
zCloak Network is a private computing service platform based on the Polkadot ecosystem, which uses the zk-STARK virtual machine to generate and verify zero-knowledge proofs for general computing. Based on the original autonomous data and self-certifying computing technology, users can analyze and calculate data without sending data externally. Through the Polkadot cross-chain messaging mechanism, data privacy protection support can be provided for other parallel chains and other public chains in the Polkadot ecosystem. The project will adopt the "zero-knowledge proof-as-a-service" business model to create a one-stop multi-chain privacy computing infrastructure.