在區塊鍊網絡中，節點如何確保新提出的區塊的所有數據都是可用的？這為什麼重要？

在這篇文章中，我們將深入探討數據可用性問題及其如何影響以太坊的擴展性。

數據可用性問題是什麼？

數據可用性（DA）問題：區塊鍊網絡中的節點如何確保新提出的區塊中的所有資料實際上是可用的？如果資料不可用，該區塊可能包含由區塊生產者隱藏的惡意交易。即使區塊包含非惡意交易，隱藏它們也可能威脅到系統的安全。

例如，假設Alice 是一個ZK-Rollup 的經營者。她在以太坊上提交了一個ZK-Proof 並得到驗證。如果她沒有在以太坊上提交所有交易數據，儘管她的證明證實了在rollup 中進行的所有狀態轉換都是有效的，但rollup 的用戶仍可能對他們當前的賬戶餘額一無所知。因為零知識的特性，提交的證明無法揭示當前狀態的信息。

在Optimistic Rollup 的場景中，也存在類似的例子，其中Alice 在以太坊上提交了一個聲明（assertion），但由於交易資料不可用，OPR 的參與者無法重新計算或質疑該聲明。

為了應對上述情況，OPR 和ZKR 的設計都要求業者將所有交易細節作為「calldata」提交到以太坊上。雖然這使它們在短期內避免了DA 問題，但隨著rollup 內部交易數量的增加，需要提交的資料量也會增長，限制了這些rollup 能夠提供的擴展量。

更糟的是，數據不可用是一種無法唯一歸因的錯誤。這意味著參與者無法向其他節點證明特定資料塊缺失。這是因為Bob 可以廣播Alice 提交的區塊缺少數據，但當Charlie 向Alice 詢問時，她可能會提供數據給他。

數據可用性問題怎麼影響目前的區塊鏈？

為回答這個問題，讓我們先回顧一下類似以太坊的區塊鏈的一般區塊結構，以及任何區塊鍊網絡上存在的客戶類型。

一個區塊可以分為兩個主要部分：

• 區塊頭：一個小的區塊頭包含與區塊中包含的交易相關的摘要和元資料。

• 區塊體：包含所有交易數據，構成區塊的主要部分。

在傳統的區塊鏈協議中，所有節點都被視為完整節點，它們同步整個區塊並驗證所有狀態轉換。它們需要花費大量資源來檢查交易的有效性並儲存區塊。優點是，這些節點不會接受任何無效的交易。

可能還有另一類節點，它們沒有（或不想花費）資源來驗證每筆交易。相反，它們主要對了解區塊鏈的當前狀態和一些對它們有關的交易是否被鏈包含感興趣。理想情況下，這些輕客戶端也應該被保護不受包含無效交易的鏈的欺騙。這實際上可以使用所謂的詐騙證明來實現。這些簡潔的信息顯示特定的區塊體包含無效的交易。任何完整節點都可以產生這樣的詐騙證明，因此輕客戶端不必信任某個特定的完整節點是誠實的。它們只需確保它們與一個能夠確保如果有區塊頭的欺詐證明可用，它們將接收到它的八卦網絡連接良好。

然而，這個系統存在一個問題：如果一個區塊生產者不透露一個區塊背後的全部數據呢？在這種情況下，完整節點顯然會拒絕這個區塊，因為在它們看來，如果一個區塊不附帶區塊體，那麼它甚至不是一個區塊。然而，輕客戶端可以被展示區塊頭鏈，並且無法注意到資料缺失。同時，完整節點不能產生詐騙證明，因為它們缺少創建詐騙證明所需的資料。

為了應對這個問題，我們需要一種機制來讓輕客戶端驗證資料可用性。這將確保隱藏資料的區塊生產者不能透過說服輕客戶端來逃避。這也會迫使區塊生產者透露部分數據，使整個網路以協作的方式存取整個區塊的數據。

讓我們透過一個例子更深入地了解這個問題。假設區塊生產者Alice 建構了一個包含交易tx 1、tx 2、...、txn 的區塊B。假設tx 1 是一個惡意交易。如果tx 1 被廣播，任何完整節點都可以驗證它是惡意的，並將這個資訊作為欺詐證明發送給輕客戶端，輕客戶端會立即知道這個區塊是不可接受的。然而，如果Alice 想要隱藏tx 1 ，她就只透露頭部和除tx 1 之外的所有交易數據。完整節點無法驗證tx 1 的正確性。

有人可能會認為一個簡單的解決方案是讓所有輕客戶端隨機抽樣交易，如果他們發現他們的樣本是可用的，他們就可以確信區塊是可用的。但讓輕節點隨機查詢任一筆交易，輕客戶端查詢tx 1 的機率是1/n。因此，Alice 幾乎總是能欺騙輕客戶端接受一個惡意交易。換句話說，大多數輕客戶端都會被欺騙。由於不可歸因的性質，完整節點無法以任何方式證明tx 1 是不可用的。不幸的是，增加樣本數也並不能使情況變得更好。

那麼，我們該如何解決這個問題呢？

解決這個問題的方法在於在區塊中引入冗餘。在編碼理論，特別是擦除編碼方面，有一套豐富的文獻可以幫助我們解決這個問題。

簡而言之，擦除編碼允許我們將任何n 個資料區塊擴展成2 n 個資料區塊，這樣任何2 n 中的n 個就足以重構原始資料（參數是可調的，但這裡我們為了簡化而考慮這種情況）。

如果我們迫使區塊生產者對交易tx 1、tx 2、...、txn 進行擦除編碼，那麼要隱藏單一交易，它需要隱藏n+ 1 個資料區塊，因為任何n 個資料區塊都足以建構整個交易集。在這種情況下，少量的查詢就能讓輕客戶端非常有信心地知道底層資料確實是可用的。

Woah,所以就這樣嗎？

不。儘管這個簡單的技巧使隱藏資料變得更加困難，但仍有可能區塊生產者故意以錯誤的方式進行擦除編碼。然而，完整節點可以驗證這種擦除編碼是否正確進行，如果沒有，它可以向輕客戶端證明這一點。這就是另一種類型的詐騙證明，就像上面提到的惡意交易一樣。有趣的是，只需一個誠實的完整節點作為輕客戶端的鄰居，就能確保如果區塊是惡意的，那麼它將收到一個欺詐證明。這確保了輕客戶端能夠以非常高的機率訪問一個沒有惡意交易的鏈。

但有一個問題。如果做得太簡單，一些詐騙證明的大小可能會和區塊本身的大小一樣大。我們對輕客戶端的資源假設禁止我們使用這樣的設計。通過使用多維擦除編碼技術，已經有了改進，這些技術降低了詐騙證明的大小，但代價是增加了承諾的大小。為了簡潔起見，我們不在這裡詳細介紹這些，但這篇論文對此進行了詳細的分析。

基於詐騙證明的解決方案的問題在於，輕客戶端永遠無法完全確定任何它尚未收到詐騙證明的區塊。同時，它們繼續信任其完整節點是誠實的。誠實的節點也需要激勵，以持續審核區塊。

我們在這裡關注的是那些系統，它們保證如果區塊編碼無效，完整節點可以檢測到並向輕客戶端提供證明，以說服它們存在不當行為。然而，在下一部分中，我們將關注那些保證只有有效編碼才能被提交到鏈上的區塊編碼。這消除了需要證明編碼錯誤的詐騙證明的需求。基於有效性證明的解決方案使應用程式能夠在不必等待完整節點提供此類詐騙證明的情況下使用系統。

那麼，這些解決方案是如何運作的呢？

近期，多項式承諾在區塊鏈領域引起了重新的興趣。這些多項式承諾，特別是對多項式的恆定大小的KZG/Kate 承諾，可以用來設計一個不需要欺詐證明的整潔的數據可用性（DA）方案。簡而言之，KZG 承諾允許我們使用單一橢圓曲線群元素來承諾一個多項式。此外，此方案支持我們證明在某一點i 上，多項式φ 的值為φ(i)，使用恆定大小的見證。這種承諾方案在計算上是約束性的，也是同態的，允許我們巧妙地避開詐騙證明。

我們強制區塊生產者將原始交易資料排列成一個大小為nxm 的二維矩陣。它使用多項式插值將每個列的大小n 擴展為大小2 n 的列。這個擴展矩陣的每一行產生一個多項式承諾，並將這些承諾作為區塊頭的一部分發送。下面給出了區塊的示意性表示。

輕客戶端查詢這個擴展矩陣的任何一個單元格以獲取證明，這使得它能夠立即根據區塊頭進行驗證。恆定大小的成員證明使得取樣極為有效率。承諾的同態特性確保只有在區塊構建正確時，證明才能被驗證，而多項式插值確保了恆定數量的成功樣本意味著數據可用性的可能性非常高。

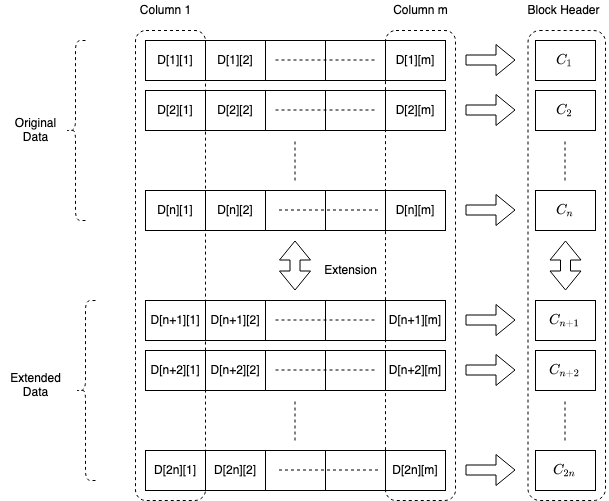
區塊的示意性表示

這個方案的更細節部分，以及進一步的優化和成本估算，超出了本文的範圍。然而，我們想指出的是，雖然我們在這裡討論的是一個二維方案，但類似的保證也可以透過一個一維方案提供，一維方案的區塊頭大小更小，但代價是減少了並行性和輕客戶端採樣效率。我們將在後續文章中更深入地探討這一點。

其他替代方案是什麼？接下來會發生什麼事？

高維度擦除編碼和KZG 承諾並不是解決資料可用性問題的唯一方法。我們在這裡略過了其他一些方法，例如編碼默克爾樹、編碼交錯樹、FRI 和基於STARK 的方法，但每種方法都有其優點和缺點。

在Avail，我們一直在使用KZG 承諾開發數據可用性解決方案。在後續的文章中，我們將介紹實作細節，如何使用它，以及我們如何規劃改變資料可用性問題空間。欲了解更多關於Avail 的信息，請在Twitter上關注我們，並加入我們的Discord 服務器。

Twitter：https://twitter.com/AvailProject

Discord：https://discord.com/invite/jTkvDrZ54r

也歡迎追蹤Modular 101 的Twitter 帳號：@Modular 101