原文作者:Xiang|W3.Hitchhiker
原文作者:Xiang|W3.Hitchhiker
 原文編輯:Evelyn|W3.Hitchhiker
原文編輯:Evelyn|W3.Hitchhiker
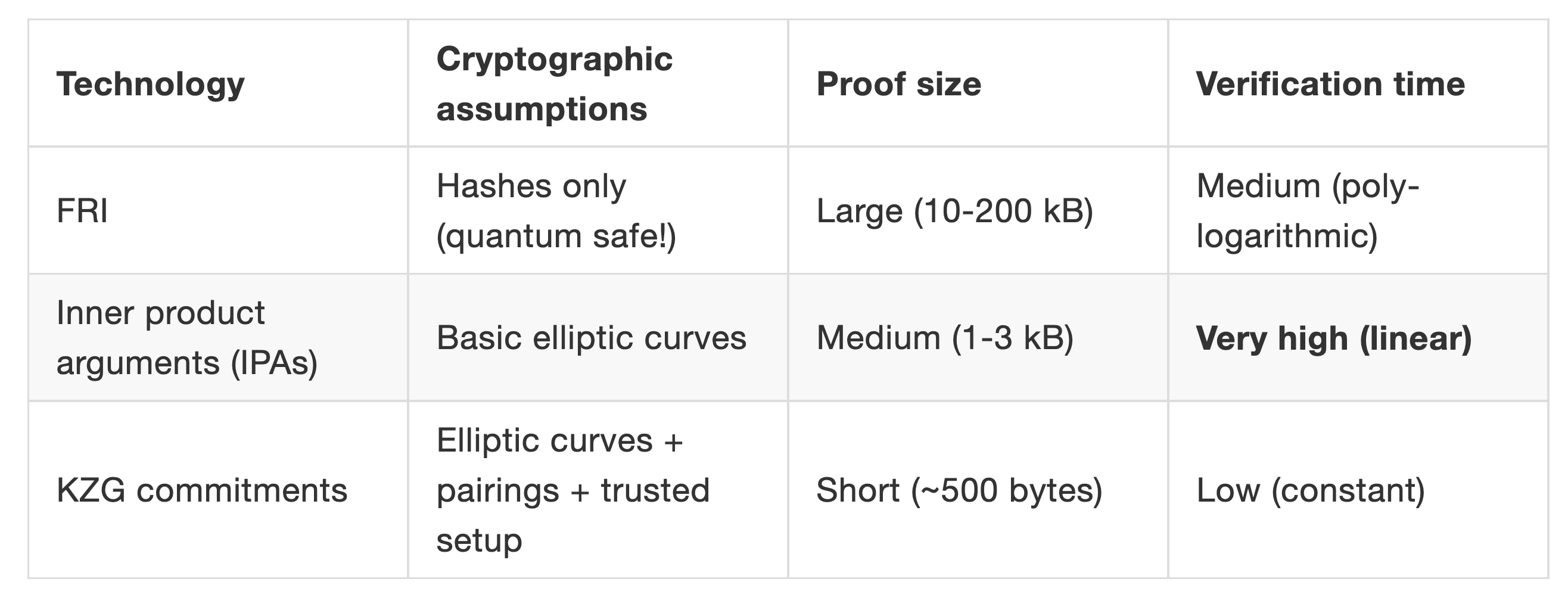
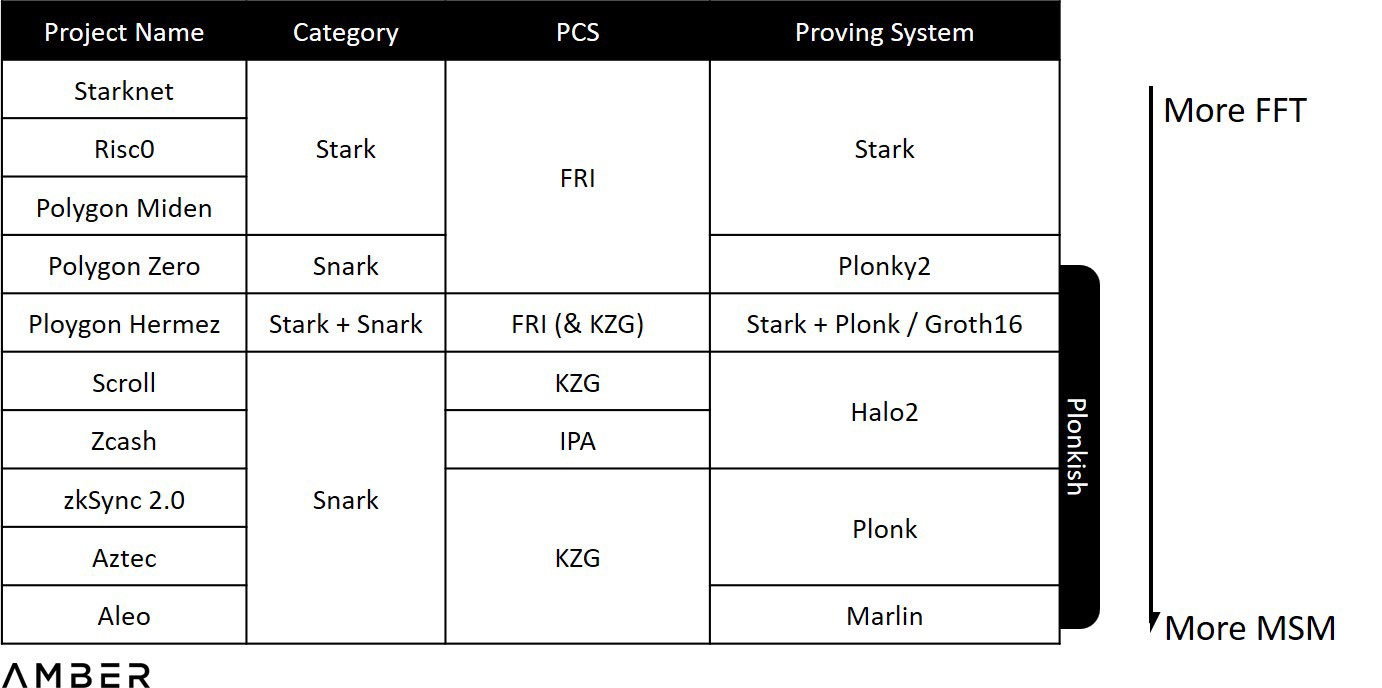
不同多項式承諾方案列表
上表中,FRI 是Starkware 採用的多項式承諾方案,可以實現量子級別的安全,但證明的數據量卻是最大;IPA 是Bulletproof 和Halo2 零知識算法默認的多項式承諾方案,驗證時間相對較長,採用的項目有門羅幣,zcash 等,前兩者是不需要初始可信設置的。
二級標題
二級標題
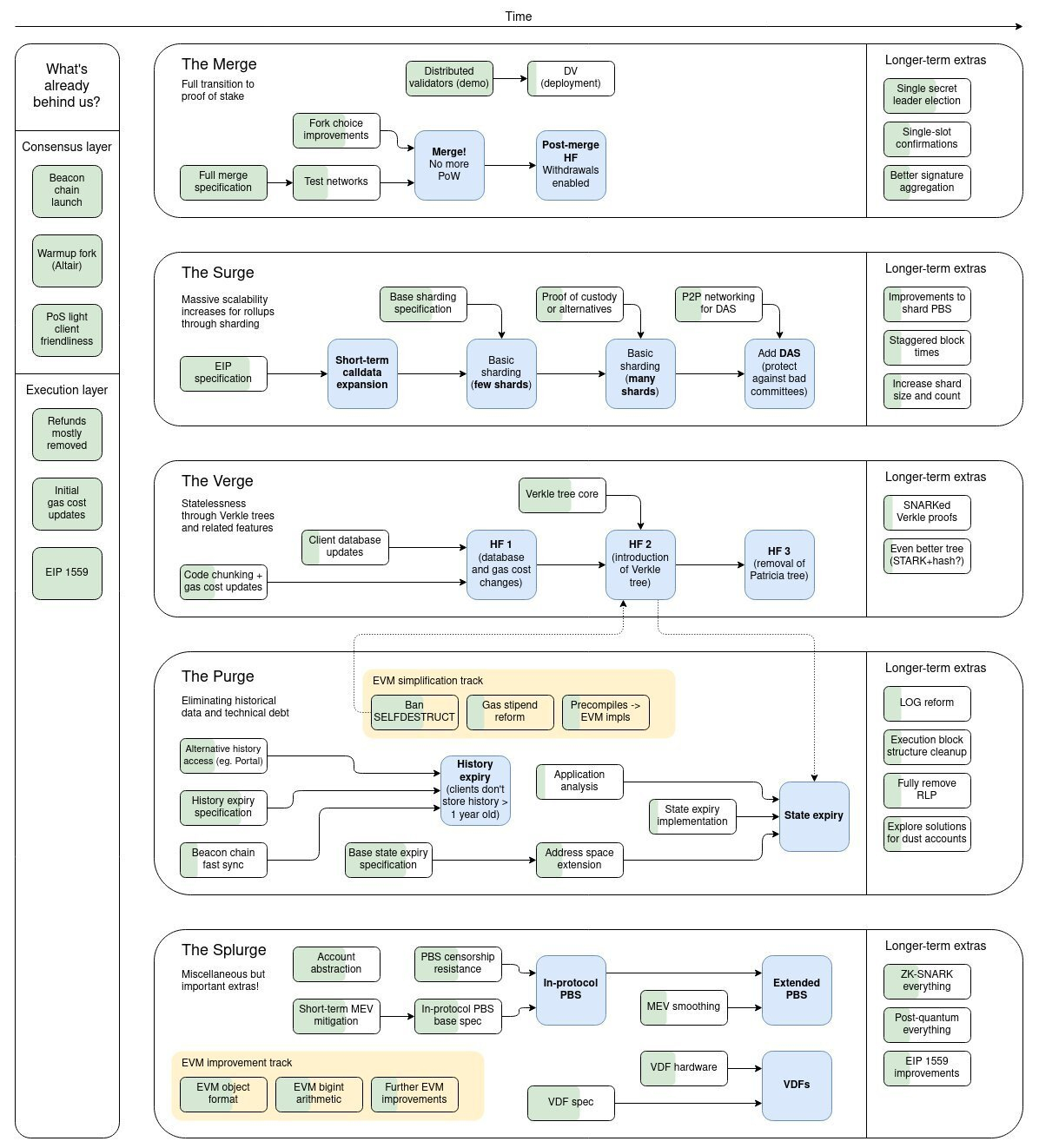
The Merge:
二級標題
The Surge:
二級標題
The Verge:
二級標題
The Purge:
二級標題
The Splurge:
二級標題
四個不同部分升級後的協調,旨在減少錯誤(Bugs) 的出現和確保網絡能暢順運作,還有就是EVM 改進和添加賬號抽像模型等。
其中The Surge 升級將藉鑑多項式承諾技術實現數據可抽樣性功能,The Verge 升級將利用多項式承諾來優化其數據結構,ETH L2 的zkrollup 也都採用了多項式承諾來實現其零知識證明帶來的性能拓展。
什麼是KZG 多項式承諾
此文這裡只介紹較好理解的KZG 多項式承諾,KZG 多項式承諾(KZG Polynomial Commitment)也被稱為卡特多項式承諾方案,是Kate,Zaverucha 和Goldberg 一起發表的。在一個多項式方案中,證明者計算一個多項式的承諾,並可以在多項式的任意一點進行打開,該承諾方案能證明多項式在特定位置的值與指定的值一致。
之所以被稱為承諾,是因為當一個承諾值(橢圓曲線上的一個點)發送給某對象(驗證者)時,證明者不可以改變當前計算的多項式。他們只能夠對一個多項式提供有效的證明;當試圖作弊時,它們要不無法提供證明,要不證明被驗證者拒絕。
KZG 數學原理二級標題。
一級標題

二級標題

二級標題
單個證明

卡特證明單個數據的公式推衍如下,由於橢圓曲線群只支持加法同態,無法支持多項式之間的乘法,這是就需要通過配對函數解決,

由於橢圓曲線群並不支持運算多項式之間的乘法運算,所以此時得採用配對函數去解決
批量證明
具體應用場景
多項式承諾應用方向總結起來可以分為3 大類
數據可用性(ETH Surge 升級,ETH danksharding,降低L2 成本,模塊化數據可用性項目Avails)
數據結構優化(MPT 樹改為Verkle 樹,ETH Verge 升級,無狀態客戶端,實現ETH 的輕量的驗證節點)
零知識證明系統(Zksync,Zkswap,Scroll,PSE 給Zk 提供多項式承諾方案,大大提升鏈的拓展能力)
1. 數據可用性
DAS (數據可用性抽樣)
核心目的:數據缺失則無法通過大多數節點抽查
盡力做到:佔用帶寬小,抽樣過程所需計算量小
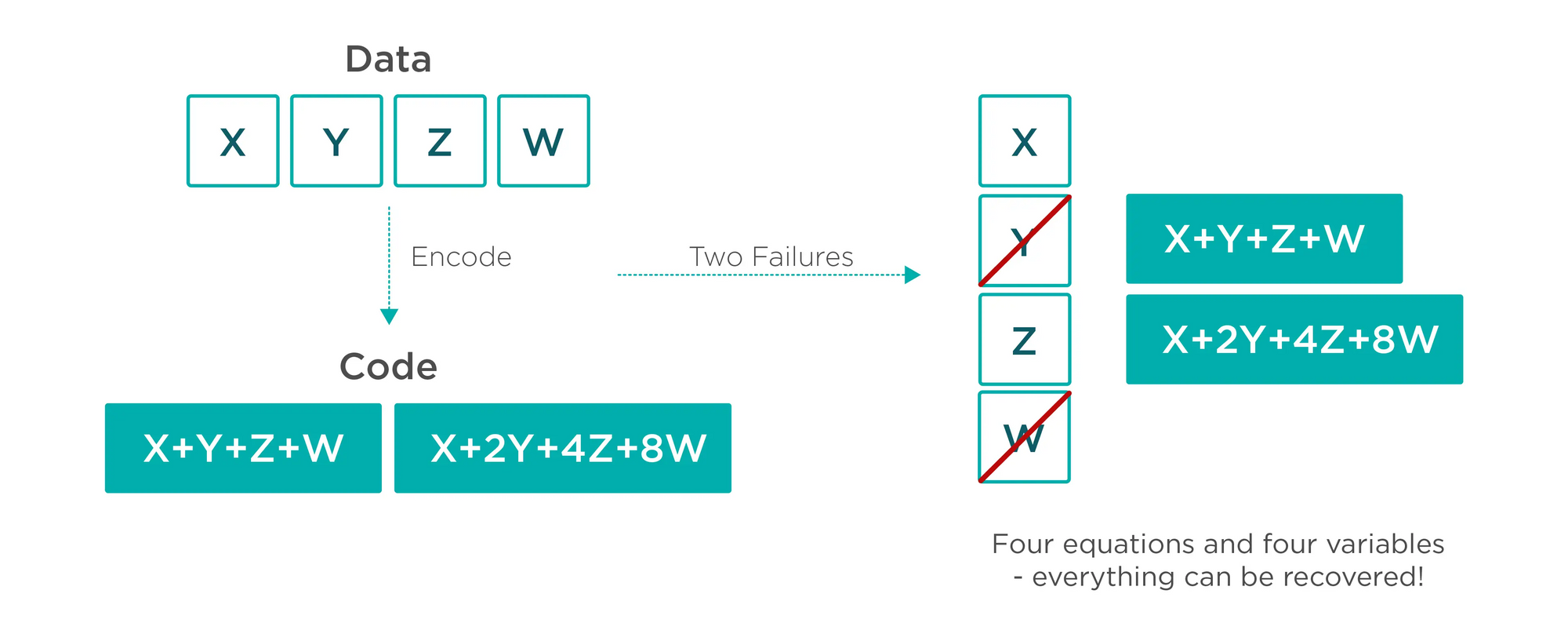
糾刪碼(celestia)
糾刪碼會增加額外數據塊,這種情況很容易通過抽樣調查發現,從而提升安全性。
以上圖為例,有4 個數據,一次只能抽樣一個,假設一個數據有問題,每個用戶抽樣發現錯誤的概率是1/4,但是加入兩數據塊後,還是一個數據有問題,用戶抽樣發現的概率可以高達1/2(3/6)。這樣就能大幅提升安全性。
KZG 也可實現糾刪碼,利用拉格朗日公式:
比如把(0,3),(1,6) 帶入公式可得,y=3x+3
y1,y2 可以理解為要保存的數據,
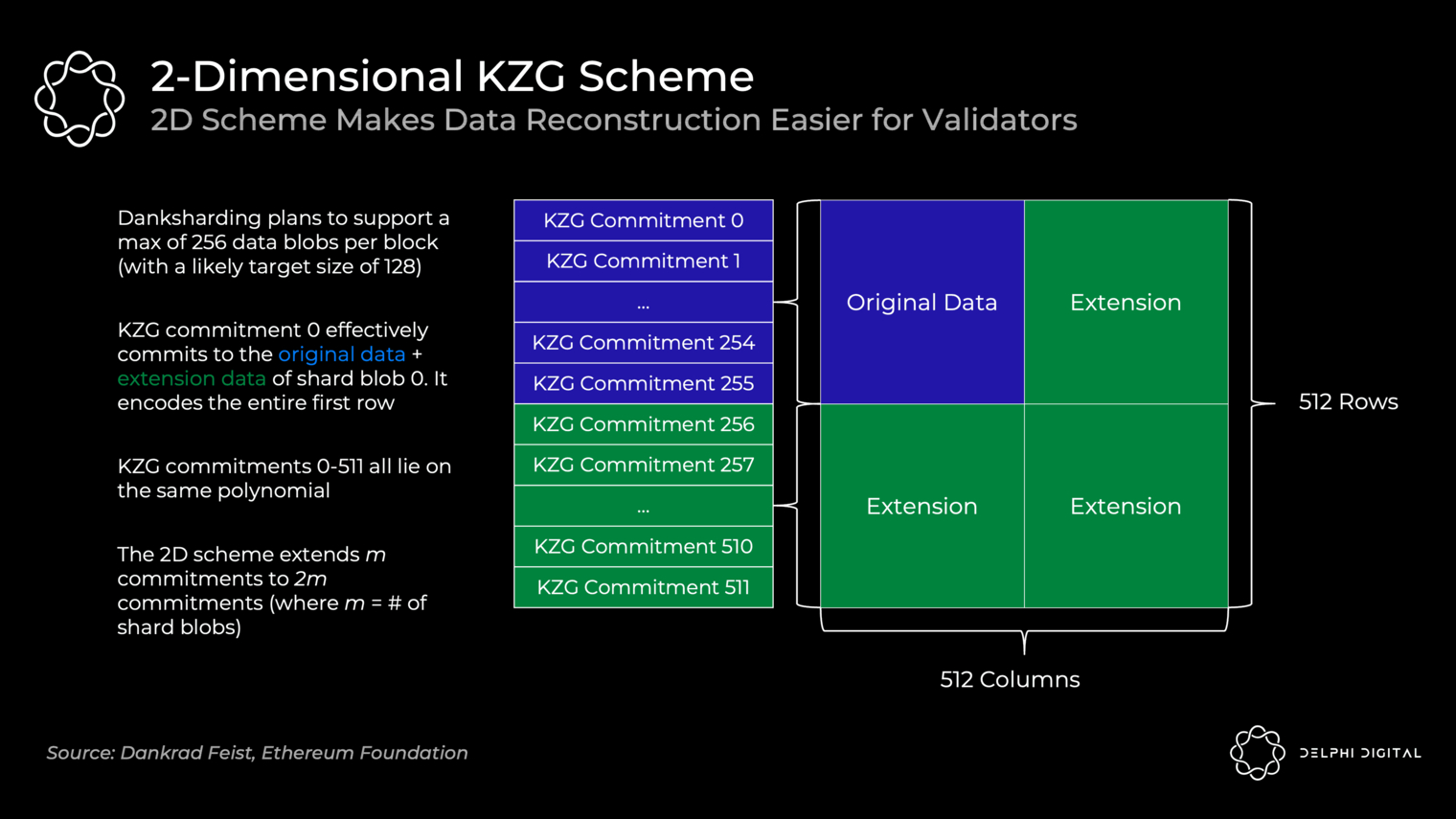
對應點(2,8)(3,12) 等等,其中y 值可以作為糾刪碼數據,其中任意兩個點都可以推出原多項式公式係數。
不同數據可用性項目組成
Celestia = Tendermint (cosmos) + 2d 糾刪碼+ 欺詐證明+ Namespace merkle tree + IPFS 基礎設施(數據存儲用的IPFS Blockstore,傳輸網絡用的IPFS 的Libp2p 與bitswap,數據模型用的IPFS 的Ipld)
ETHprotoDankSharding = Blobs 數據(數據可用性的存儲,替換現有的calldata)+ 2d 糾刪碼+ KZG 多項式承諾(未定,方案方案
目前仍在討論)+ ETH 基礎設施
EIP-4844 升級將在The Merge 之後的下一個以太坊分叉升級中引入“proto-danksharding”並添加blob交易類型(EIP-4844),這有望將第2 層Rollup 的可擴展性提高,同時為實現完全分片(sharding)鋪平道路。
增加一種新的交易類型,這種交易包含額外的存儲空間—— Blobs
Blob 開始只有128 KiB 的存儲空間
(1)一個交易最多包含2 個Blob,即256 KiB
(2)一個Block 最多包含16 個,即2 MiB;Target 是8 個,即1 MiB(可擴大)
Blob 以KZG Commitment Hash 作為Hash,用於數據驗證,作用和Merkle 類似
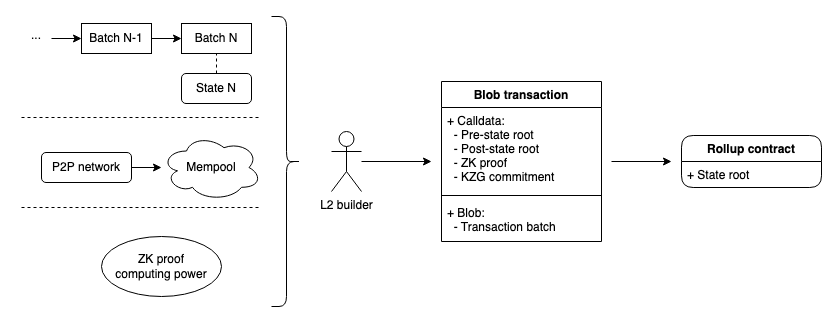
節點同步鏈上的Blob Transaction 後,Blob 部分會在一段時間後過期刪除
L2 需要通過更新目前在L1 的合約,以支持DankSharding。
Celestia 通過欺詐證明實現。當見證人發現數據沒有被正確採用刪碼技術,那麼這個人就會將欺詐證明提交從而來提醒其他節點。但是這裡需要最少誠實假設(至少連接到一個誠實節點)和同步假設(當有人給我發送欺詐證明的時候,需要確保我能在一定時間內收到通知)。
protoDanksharding 後的以太坊和Polygon Avail 則採用了KZG 多項式承諾(KZG commitments) 的方法。
KZG 多項式承諾方案,理論上要優於欺詐證明方案,帶寬需求更小,抽樣所需計算量也更小,也免去了欺詐證明中的包括少數誠實假設和同步假設等的安全假設。未來ETH 也有意引入抗後量子密碼學(參考stark,採用哈希,不在使用橢圓曲線作為基礎),避免量子計算機攻擊。
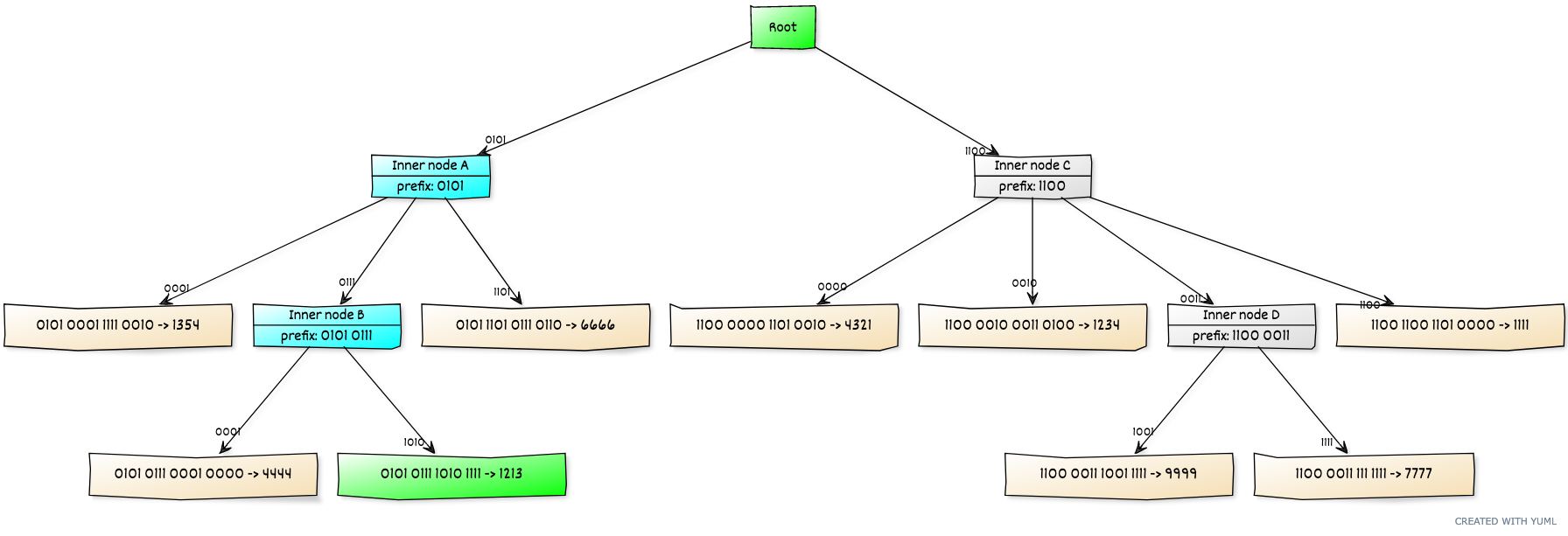
2. 數據結構優化Verkle Tree
與Merkle Tree 一樣Verkle Tree 也能實現Proof of Inclusion(PoI),而且只需KZG root 和Data 就能驗證,不需要額外的Proof,更省帶寬。
1.需求:Stateless Client
1.需求:Stateless Client
(1)節點不存完整的State Tree,只獲取需要的State 來驗證Block
(3)對State Tree 的PoI 有更高的性能要求KZG commitment
2.回顧Data Availability 裡的
每個leaf 都是polynomial 上的點
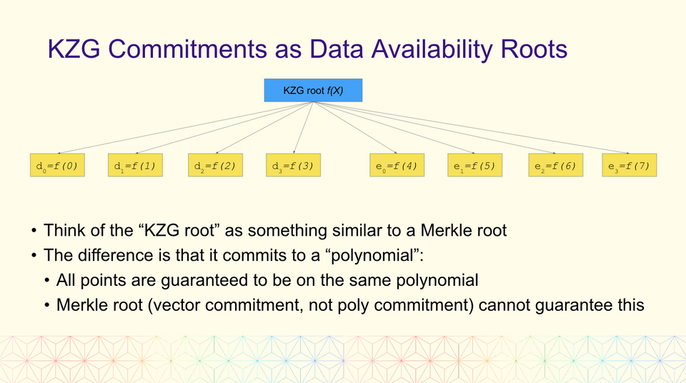
constant size proof,和leaf 數量無關
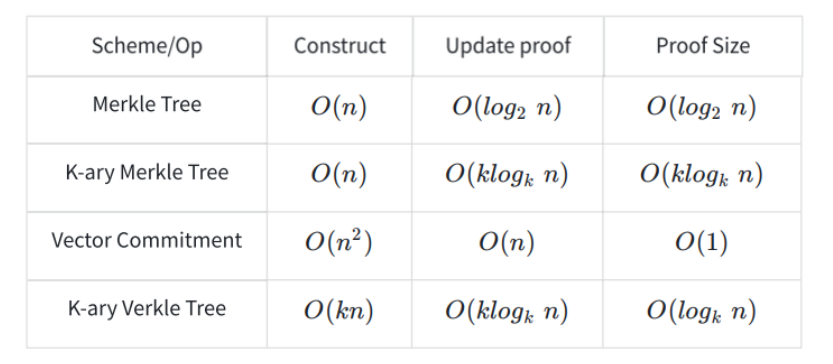

在不同樹結構中構建證明,更新證明,以及證明所需的複雜度:
Verkle 方案不需要以太坊客戶端下載完整的狀態數據,使得ETH 驗證者輕節點成為可能(甚至可支持手機運行),多項式承諾(Verkle 樹的多項式承諾方案,早期考慮的KZG,近期還是考慮用IPA )需要的證明空間複雜度大幅降低,帶寬量需求量也大幅減少。
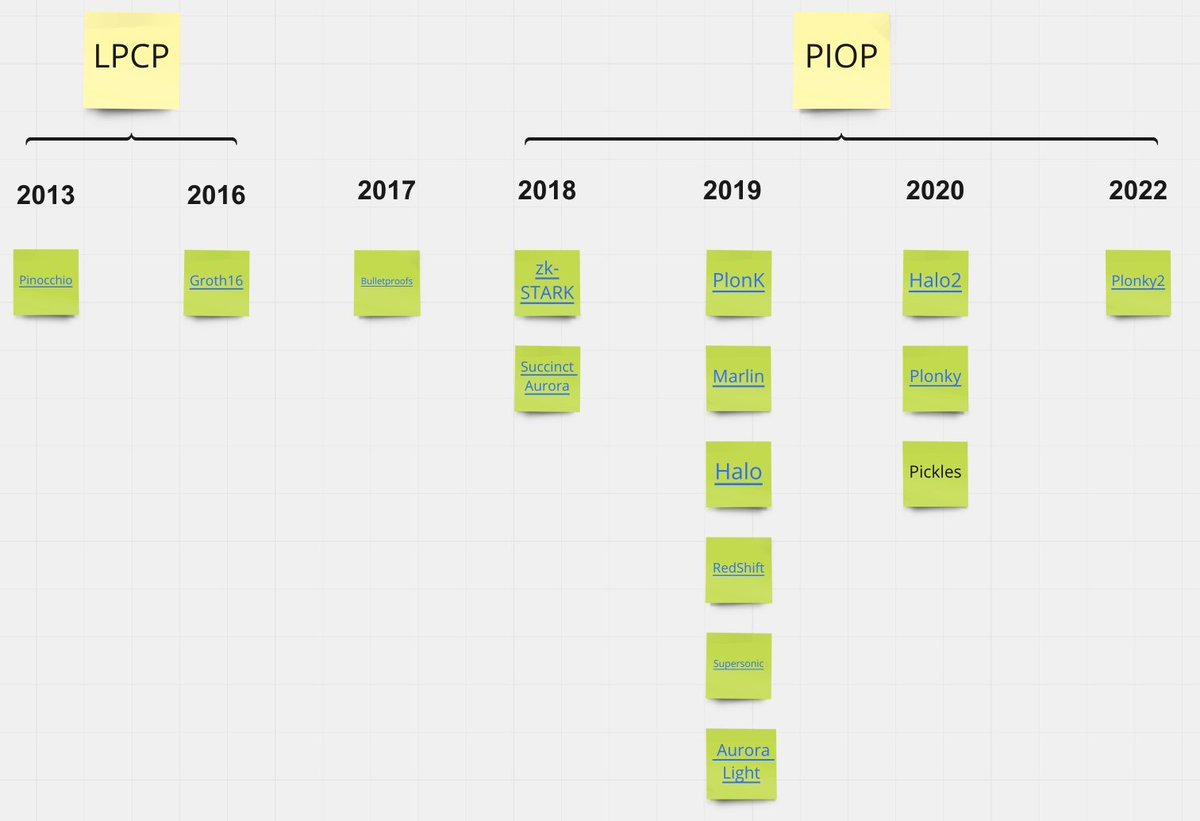
3. 零知識證明系統
早期zk 技術(Groth16)屬於線性PCP 類。除要求可信設置外,主要缺點是如果需要為不同的計算(不同的電路/多項式)提供證明,都需要一次新的設置。近期zk 技術PIOP 類支持通用初始設置和透明設置(不需要信任假設)。
新的zk 證明系統通常可以描述為PIOP(Polynomial Interactive Oracle Proof,多項式交互預言證明)+ PCS(Polynomial Commitment Scheme,多項式承諾方案)。前者可被視為是證明者用來說服驗證者的約定程序,而後者使用數學方法確保該程序不會遭到破壞。項目方可以按需修改PIOP,且可以在不同PCS 中進行選擇。
原文鏈接
原文鏈接





