原文標題：《Paths toward single-slot finality》

原文標題：《

原文標題：《

原文標題：《

原文作者：Vitalik Buterin，以太坊創始人

原文編譯：雙花(@doublespending)，ECN 社區志願者特別感謝Justin Drake，Dankrad Feist，Alex Obadia，Hasu，Anders Elowsson 和各位hackmd 匿名者對這篇文章各個版本的審校和反饋。當前，以太坊區塊需要64 到95 個slot（約15 分鐘）才能實現最終確定性。這是合理的，是在去中心化/ 最終確定性時間/ 開銷曲線上的一個折衷取值：15 分鐘不算太長，而且與現有交易所的確認時間相當，它讓用戶能夠在常規計算機上運行節點，即使因為存款大小為32 ETH ( 而不是前期要求質押的1500 ETH) 而出現了大量的驗證者。

然而，我們仍然有充分的理由把最終確定性時間縮短為

一個slot

• 。這是一篇研究現狀綜述，回顧了實現該目標的路線圖。當前以太坊staking 的運作方式及依據

• 以太坊的LMD GHOST + Casper FFG 共識是權益證明區塊鏈中流行的兩類主流共識算法間的折衷：基於鏈的共識算法：

每個slot（一個預設的時間間隔，如以太坊中的12 秒）生成一條消息（區塊）。基於鏈的共識算法最大限度地提高了參與者的數量以及減少了鏈的負載，但很容易出現分叉，而且沒有任何最終確定性的概念。

傳統的BFT ( 拜占庭容錯) 共識算法：

• 每個slot 內，除了某個驗證者生成一個區塊外，每個驗證者會生成兩條消息（「attestation」，譯者註：也就是「見證」），而且一個slot 的區塊在下一個slot開始之前實現了不可逆轉的「最終確定性」。傳統的BFT 共識算法最大限度地縮短了實現最終確定性的時間，但是以鏈的高負載和僅支持少量的參與者為代價。與單純的基於鏈的系統不同，以太坊共識算法在每個slot 都會並行對鏈頭進行數以千計的見証投票。每一個epoch（32 個slot，或6.4 分鐘），所有活躍的驗證者都有機會見證（attest）一次。兩個epoch 後，Casper FFG 最終確定性工具敲定（finalize）了區塊，自此之後，回滾該區塊需要至少三分之一的驗證者銷毀其質押存款：攻擊成本會超過400 萬ETH。這就區別於單純的傳統BFT 系統，後者在一個slot 後實現最終敲定。

• 因此，今天的以太坊實現的是：適中的最終確定時間

• ——與傳統BFT 在單個slot 完成最終確定相比時間更長，但不是幾週或幾個月，或像基於鏈的共識算法那樣未曾提供過適中的鏈負載

——每個slot 會有數千條消息，但少於使用傳統BFT 時的數十萬條信息

適中的節點數

——成為一個驗證者要求質押32 ETH：與基於鏈的共識算法相比門檻更高，在基於鏈的共識算法中即使擁有很少量的Token 也可以參與共識，但與傳統BFT 共識算法要求的超大量Token 相比門檻低很多

以太坊對更高強度鏈負載的支持是由BLS 簽名聚合的效率提升來實現的。由於這些效率的提升，能實現高強度的鏈負載( 每秒消息量的角度) 得以轉化為只需適中數據和CPU 開銷的鏈負載。

BLS 簽名聚合的工作原理是將多個簽名聚合成一個，這樣，驗證聚合後的簽名只需每個參與者進行一次額外的橢圓曲線加法（不是乘法），並且64 字節可以容納任意數量參與者的簽名，而每個參與者只需一個額外的位來存儲。

基於鏈的共識算法和傳統BFT 共識算法的結合折衷，再加上源於BLS 的純效率提升，形成以太坊當前的共識算法。

那為何要改變它呢？

在使用上述推理開發出原初的以太坊共識協議後的幾年內，我們得到了一個重大的好消息和一個重大的壞消息。

• 壞消息：混合型共識機制實際上有許多不可避免的問題

• 混合型共識機制結合了分叉選擇規則以及最終確定性工具，前者用於逐個slot 推進共識，後者用於後續敲定區塊。混合型共識機制最大的問題是：

• 用戶體驗：大多數用戶不願為交易最終確定而等待15 分鐘。當前，即使交易所也通常認為資金存入在12 到20 次確認（約3 到5 分鐘）後才「最終敲定」，儘管12 到20 次PoW 確認所提供的安全性保證也很弱（與真正的PoS 最終確定相比）。

MEV 重組：混合型共識機制仍保有這樣的實際情況——短期重組是可能的，因此為佔據近多數或多數的惡意驗證者共謀重組區塊鏈來提取MEV 價值敞開大門。這篇文章更為詳盡地對這個論點進行了闡述。

交互缺陷：Casper FFG 最終敲定和LMD GHOST 分叉選擇間的「接口」是重要復雜性的來源，導致了很多需要相當複雜的補丁去修復的攻擊，還有更多的弱點被時不時地發現。

其他協議複雜性：數百行規範被用於維護驗證者集合洗牌等機制。

• 好消息：超大規模的驗證者集合因BLS 聚合變得比想像中更有可能

• 在過去三年內，BLS 實現的具體效率得到了突飛猛進的提升，同時我們掌握了更多高效地處理組合大量消息和數據的知識。

使用BLS 支持大量驗證者面臨著兩個主要的瓶頸：

最後的驗證：驗證來自N 個驗證者的簽名需要多達N/2 次ECADD 來計算群公鑰，並需要N 位（N/8 字節）的位域來存儲參與者。實際上，由於view-merge （視域合併）需要冗餘的聚合者，這些數值需要增加多達16 倍。

聚合：將N 個驗證者各自發送的簽名組合為一個聚合簽名。這需要總共至少96*N 個字節的帶寬來處理，並且需要至少N 次在G2 群之上的ECADD （多於4 倍計算強度），但分配到各個子網中會更為簡單。

實際上，最後的驗證擴展能力很強。單次ECADD 可以在約500 毫微秒(ns) 內完成，因此100 萬次ECADD 將花費約500 毫秒(ms)。 100 萬驗證者位域的大小僅為128 kB。

view-merge 的冗餘可能需要每個slot 驗證多達16 個單獨的簽名；這將數據存儲需求提升到仍然可控的2 MB（大致等於EIP-4844 中每個區塊blob 數據的大小上限，以及當前每個區塊calldata 大小上限），同時在最壞情況下ECADD 運算成本增加約8 倍（由於巧妙的預計算技巧，不用增加16 倍）。

這些是最壞情況下的數值；在通常情況下，16 個聚合者的位域是基本一致的，這讓多個聚合的主要額外成本得以壓縮。

聚合更具挑戰性，但也是相當可行的。最新研究大大加深了我們對如何在一個slot 內聚合大量簽名的理解。好消息是，我們有充分的理由相信，每個slot 處理數十萬的簽名是可能的，儘管仍需更深入的研究工作來確定和商定最佳解決方案。

• 這兩個事實結合在一起意味著，權衡的結果不再傾向於在基於鍊和基於BFT 的PoS 間進行折衷，而是更接近完全的傳統BFT 路線的解決方案，即在下個區塊開始前敲定每個區塊。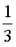我們需要解決哪些關鍵問題以實現單個slot 最終確定性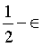？共有三個關鍵問題：。

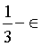• 開發確切的共識算法：我們不太能接受Tendermint 或其他現有的BFT 算法，因為我們十分看重這一點：即使在大於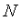驗證者離線的情況下，區塊鏈仍然能夠保持活性（這是傳統BFT 無法提供的）。我們需要添加一個分叉選擇規則、怠工懲罰（inactivity leak）和恢復機制來實現這種活性。理想情況下，我們能夠獲得最佳的安全性：網絡同步時，容錯率為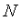；當網絡不同步時，容錯率為

• 確定最優聚合策略。對於盡可能高的

，我們想聚合來自

個驗證者的簽名並將其打包進一個塊內，而且節點開銷是我們願意接受的水平。

確定驗證者的經濟模型。儘管聚合和最後的驗證這兩個步驟有所改進，單個slot 實現最終確定性的以太坊可能最終能夠支持的的驗證者數量理論上限比當前的以太坊更小。如果這個數值最終低於欲參與的驗證者數量，我們該如何限制參與，以及我們會做出什麼樣的犧牲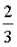？確切的共識算法會是怎樣的？

如上所述，我們想要一個遵循Casper FFG + LMD GHOST「最終確定鏈+ 樂觀鏈」範式的共識算法，在極端條件下，樂觀鏈可以回滾，但最終確定鏈永遠不能回滾。

這需要一個與分叉選擇規則和最終確定性工具與現有共識類似的結合，但其中有一個關鍵的區別：當前，我們通常會同時運行分叉選擇規則與最終確定性工具，但在單個slot實現最終確定性的世界中，我們會要么運行分叉選擇規則，要么運行最終確定性工具：如果小於

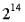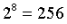的驗證者在線並且誠實地工作，那麼運行前者；否則，運行後者。對該算法的具體提案仍在進行中；目前仍未發布正式的成果或文章。開發一個最優的聚合策略會面臨哪些問題？先讓我們看看當前是如何進行聚合的。在單個slot 內，約有

個驗證者，這些驗證者被劃分為

個委員會，每個委員會約有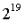個驗證者。首先，每個委員會中的驗證者在該委員會專用的p2p 子網中廣播他們的簽名。每個委員會中有16 個指定的聚合者，每個聚合者將看到的所有簽名合併為一個聚合簽名（96 字節+ 256 字位的位域）。指定的聚合者將其聚合簽名發佈到主子網中。

• 然後，區塊提議者從每個委員會中挑選最佳的（即參與者總餘額最大）聚合簽名，並將其打包進區塊。有了view merge 分叉選擇的補丁，它們還會添加一個包含其他聚合簽名的跨鬥(sidecar) 對象；只要每個委員會中至少有一個聚合者是誠實的，就可以保護view merge 機制免受惡意聚合者的影響。

• 如果我們想把這個模型擴展到單個slot 實現最終確定性的場景，那麼我們需要能夠在每個slot 之內處理所有的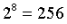( 或無論我們有多少) 個驗證者。這需要在以下兩種取捨中取其一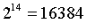：增加單個委員會的驗證者數量或者增加委員會數量，或兩者兼而有之，以適應更多的驗證者。

轉向三層聚合，兩層委員會的結構。首先，簽名先劃分成大小為

的小組進行聚合，然後大小為

的小組，最後是完整的驗證者集合。

前者要求更大的p2p 網絡帶寬，後者要求接受更高的延遲，更多的p2p 子網層級帶來更高的風險以及額外複雜性來確保view merge 免受所有層級中的惡意聚合者所影響。對這兩種策略的分析研究在持續進行中。當前，以太坊有著約

甚至更高。

個活躍的驗證者（準確來說，在本文撰寫時為445064 個），每個驗證者都質押了32 個ETH。到單個slot 最終確定性實現時，驗證者數量可能會增加到

甚至更高。

這帶來了一個重大問題：如果我們每個slot 只能處理來自N 個驗證者的簽名，但如果有超過N 個以上的驗證者想要參與，那麼我們該如何確定誰去誰留？

這是一個重大問題，因為任何方案都將涉及弱化staking 系統的一個或多個被視為安全保障的特性。

好消息：源於支持自發驗證者余額合併的收益

因為單個slot 最終確定性移除了委員會的概念（甚至danksharding 也不會使用固定大小的委員會），我們不再需要32 ETH 的驗證者有效餘額上限。考慮到p2p 網絡穩定性的因素，我們仍然想要一個更高的上限（例如，2048 ETH），但即便如此，這也意味著本來屬於富有用戶的大量驗證者槽位將會被合併成數量少得多的驗證者槽位。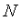我們可以用Zipf 定律估計整合富有用戶的驗證者slot 的收益：某個擁有特定餘額的質押者數量與其餘額成反比（因此餘額為100-2000 ETH 的質押者數量是餘額為1000-2000 ETH 的質押者數量的10 倍）。使用了信標鏈的早期歷史數據，Zipf 定律似乎相當準確地擬合了分佈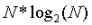：假設符合Zipf 定律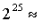，個質押者將擁有大約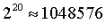個ETH，那麼今天就需要

個驗證者槽位。把

3350 萬ETH 填入該式子，我們可以得到共計65536 個質押者，在今天的以太坊則需要消耗

個驗證者槽位。因此，完全移除有效餘額上限讓需要處理的驗證者槽位數量減少到65536 個，而維持2048 ETH 的上限（提升自當前的32 ETH）只會額外增加約1000 到2000 個驗證者。只需將聚合性能提升約2 倍或讓負載增加約2 倍，就能夠處理當前情況下的單slot 最終確定性！

作為一個附帶的好處，這也對小型質押者更加公平，因為小型質押者可以質押全部餘額而不是一部分（例如，當前擁有48 ETH 的人只能質押其2/3 的ETH）。質押獎勵將自動被重新質押，即使是小型驗證者也能從復利中獲益。事實上，出於這個原因，把質押上限提高到2048 ETH 甚至可能是一個好主意！

然而，我們仍需要處理例外情況：（i）驗證者余額分佈不再符合Zipf 定律，或（ii）富有的驗證者不打算合併其餘額，或（iii）質押了超過3300 萬的ETH。

我想到了處理這些情況的兩種現實策略：超級委員會和設定驗證者集合大小上限。

思路1：超級委員會

不是所有驗證者都參與每一輪Casper FFG，而是只有一個由數萬人組成的中型超級委員會參與，讓每輪共識都在一個slot 內發生。

這一技術思路在這篇帖子中首次介紹。這篇帖子更加詳細地描述了該思路，但其核心原則很簡單：在任何給定的時間，只有一個從完整驗證者集合隨機抽樣得到的中型超級委員會（例如，價值4 百萬ETH）被激活。每次鏈達到最終確定性，委員會都會改變，其中多達25% 的成員會被隨機採樣的新驗證者替換。

在該策略中，「誰留誰走？」就是：每個人都會逗留一部分時間，而在另一部分時間離開。

• 超級委員會得有多大？

• 這個問題可以歸結為一個更簡單的問題：51% 攻擊以太坊需要多少代價？理想情況下，由於攻擊被罰沒以及怠工懲罰的ETH 數量需要大於從攻擊中實際獲得的收益。攻擊的成本甚至應該足夠高，從而讓那些有強烈外部動機去毀滅這條鏈的強大攻擊者受到威懾或損失慘重。

• 回答實現這一目標需要多少ETH 這一問題不可避免地要依賴直覺。以下是一些我們可以問的問題：

• 來自Justin Drake 的估算表明，當前對比特幣進行spawn-camp 攻擊（即持續進行51% 攻擊直到社區改變PoW 算法）的成本約為100 億美元，或比特幣市值的1%。對以太坊進行一次51% 攻擊的成本應該是該水平的多少倍？

圖片描述

圖片描述

圖片描述

以太坊研究員的內部投票

• 如果我們僅關注不依賴網絡延遲的51% 攻擊，100 萬枚ETH 的攻擊成本意味著200 萬枚ETH 規模的超級委員會（約65536 個驗證者）。如果我們還考慮涉及惡意驗證者和網絡操縱的複雜組合的34% 攻擊，那麼規模為300 萬枚ETH ( 大約97,152 個驗證者)。

• 複雜性成本

• 除了降低攻擊成本以外，該方案的另一個主要弱點是複雜性，包括協議複雜性和分析複雜性。特別是：

我們需要數百行規范代碼來選舉超級委員會並進行輪換。

富有的驗證者會在多個驗證者槽位間分配其ETH 以減少收益波動，因此我們會因提高有效餘額上限失去了一些好處。

• 若出現臨時性的高手續費或高MEV，超級委員可能會故意拖延最終確定性的達成來避免被換出，從而可以繼續收取手續費和MEV。

• 思路2：設置驗證者集合規模上限

我們可以試著採用兩類設置上限方案中的一種（或兩種）：

設置ETH 質押總量上限

• 設置驗證者總量上限

• 每種設置上限的方案都可以選擇基於順序的機制( 堆棧或隊列) 或經濟模型調節的機制來實現。

基於順序的機制有著很多問題。要了解其中原因，可以考慮兩類基於順序的策略：

保留最舊的驗證者（OVS）：如果驗證者集合已滿，那麼其他人無法加入

保留最新的驗證者（NVS）：如果驗證者集合已滿， 那麼最舊的驗證程序將被踢出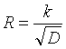這兩類都有著嚴重的問題。 OVS 有著轉向一個早期質押者盤踞其中的「王朝」的風險，質押者一旦離開，則可能會永遠失去再加入的機會。這也會導致每當某個驗證者離開都會出現MEV 拍賣或排著長隊以加入驗證者集合。另一方面，NVS 可能會引發持久的MEV 競拍，這會幹擾整條鏈，因為被踢出的驗證者會想立即重新加入，從而與真正的新參與者進行競爭。

另一種可選機制是使用經濟學模型設置上限：如果存在過多的驗證者想參與，那麼懲罰所有新舊驗證者，直至某些驗證者放棄並離開。一個簡單的方法是將驗證者獎勵公式從當前的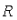其中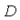更改為形如：

其中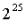是對錶現良好的驗證者的獎勵（表現不佳的驗證者會獲得相對較低的獎勵），而

是當前活躍驗證者的ETH 總餘額。該曲線大致如下：

在曲線的左側，驗證者獎勵起到與當前機制一致的作用。但是，隨著ETH 質押總量增加到數百萬，獎勵函數開始加速下降，在約2500 萬ETH 時，獎勵會降至零以下。在優先費用（priority fee）和MEV 收益足以覆蓋其損失的特殊情況下，儘管基本收益為零或負數，驗證人可能會願意繼續質押。獎勵曲線在

ETH（約3350 萬ETH）處趨於負無窮，從而無論外部獎勵有多高，驗證者集合的大小無法越過該上限。

該方法的優勢在於它完全避開動態隊列的設計：無論均衡點在哪裡，它都能達到均衡；驗證者集合大小最終會達到均衡點（在當前條件下，沒有更多的驗證者想要參與）。

該方法的主要缺點是在曲線右側附近持續進行阻攔攻擊：攻擊者可以加入并快速趕出其他驗證者。但這是相對其他方案而言的一個小問題，因為它只能在MEV 異常高的情況下發生，而且這種攻擊非常昂貴（需要數百萬枚ETH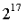）。另一個主要缺點是，它可能使得我們趨於一個大多數驗證者都被「邊緣化」的未來，大型質押者由於更能容忍收益波動，從而在競爭中會勝過小型質押者。

通過經濟模型設置驗證者總量上限

通過添加正比於驗證者總量的懲罰項，我們可以使用相同的邏輯來設置驗證者總量上限。例如，如果我們想要設置的驗證者上限為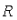，我們可以這樣做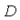：另一種方法是添加浮動最低餘額：如果驗證者總量超過上限，則將擁有最低餘額的驗證者踢出。

浮動最低餘額會面臨一類新型的惡意攻擊的挑戰：富有的驗證者劃分他們的質押資金，以便踢走小型驗證者（從而增加了他們的獎勵

• ，因為質押總量

• 減少了）。我們可以通過增加每個驗證者槽位的費用來緩解這一問題，並達到這樣的目的：在Zipf 分佈下，不值得進行此類攻擊。然而，如果不再服從Zipf 分佈，那麼仍會留下一個潛在的漏洞。

• 所有這些提案的一個重要問題是，它們改變了現有安全保證。尤其：

仍需仔細考慮以確定社區最能接受哪種權衡。

總結

總結

• 總結

• 總結

• 這裡有三個主要問題需要研究：

原文鏈接

原文鏈接

原文鏈接