原文編譯:南風
原文編譯:南風

使協議盡可能簡單,同時仍然使區塊鏈能夠做好一個有效的區塊鍊網絡需要做到的事情。
以太坊協議在這方面還遠遠不夠完美,特別是因為它的很多部分都是在2014-16 年設計的,當時我們對它的理解要少得多,但我們仍然在盡可能地積極努力降低複雜性。然而,這個目標的挑戰之一是複雜性很難定義,且有時,你必須在兩個引入不同種類複雜性和具有不同代價的選擇之間進行權衡。我們如何比較?(systemic complexity)。
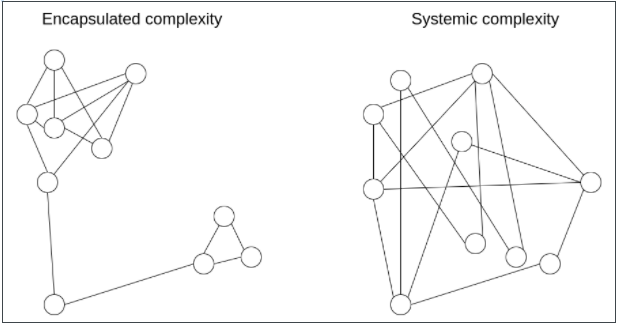
有一個強大的智能工具可以讓我們對複雜性進行更細緻的思考,那就是區分我們所謂的封裝複雜性(encapsulated complexity) 和
系統複雜性
當一個系統的子系統內部複雜,但向外部呈現一個簡單的“接口” (interface) 時,就是出現了「封裝複雜性」。當系統的不同部分甚至不能被清晰地分開,並且相互之間有復雜的交互時,「系統複雜性」就出現了。
以下是幾個例子。
BLS 簽名vs. Schnorr 簽名
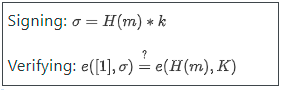
BLS 簽名和Schnorr 簽名是兩種常用的可由橢圓曲線構成的加密簽名方案。
現在,我們來看看Schnorr 簽名。 Schnorr 簽名只依賴於基本的橢圓曲線。但是簽名和驗證邏輯有點複雜:

例如:
例如:
例如:
Schnorr 簽名需要生成隨機數,BLS 簽名不需要。
二級標題
二級標題
二級標題
密碼學vs. 加密經濟學
在許多區塊鏈設計中出現的一個重要設計選擇是密碼學(cryptography) 與加密經濟學(cryptoeconomics) 的比較。這(比如在Rollups 中) 常常是在有效性證明(即ZK-SNARKs) 和欺詐證明之間做出選擇。
ZK-SNARKs 是複雜的技術。雖然ZK-SNARKs 工作原理背後的基本思路可以在一篇文章中解釋清楚,但實際上實現一個ZK-SNARK 來驗證一些計算涉及到比計算本身多很多倍的複雜性(因此,這就是為什麼用於EVM 的ZK-SNARKs 證明仍在開發中,而用於EVM 的欺詐證明已經在測試階段)。有效地實現一個ZK-SNARK 證明涉及到了對特殊目的進行優化的電路設計、使用不熟悉的編程語言以及許多其他挑戰。另一方面,欺詐證明本身就很簡單:如果有人提出挑戰,你只需直接在鏈上運行計算。為了提高效率,有時會添加一個二進制搜索方案,但即使這樣也不會增加太多的複雜性。
雖然ZK-SNARKs 很複雜,但它們的複雜性是封裝複雜性。另一方面,欺詐證明的相對較低的複雜性,是系統複雜性。以下是欺詐證明引入的一些系統複雜性的例子:
它們需要謹慎的激勵工程來避免驗證者的困境。
如果在達成共識的情況下完成,它們需要為欺詐證明提供額外的交易類型,同時還要考慮到如果許多參與者同時競相提交欺詐證明會發生什麼。
基於欺詐證明的Rollups 要求流動性提供者支持即時提款。
二級標題
二級標題
二級標題各種例子
PoW (中本聰共識):較低的封裝複雜性,因為該機制非常簡單和容易理解,但有著更高的系統複雜性(如自私挖礦攻擊)。
哈希函數:較高的封裝複雜性,但有著非常容易理解的屬性,因此系統複雜性很低。
隨機洗牌算法:洗牌算法既可以是內部複雜(比如Whisk),但卻能夠確保強大的隨機性,且易於理解;也可以是內部簡單,但卻能夠產生較弱且難以分析的隨機性屬性(比如係統複雜性)。
Verkle 樹:二級標題
二級標題
二級標題
我們如何權衡呢?
通常,封裝複雜性較低的選擇也是系統複雜性較低的選擇,因此有一個選擇顯然更簡單。但在其他時候,你必須在一種複雜性和另一種複雜性之間做出艱難的選擇。在這一點上應該清楚的是,如果是封裝複雜性,那麼其危險性就會更低。一個系統複雜性帶來的風險不是一個簡單的規範長度的函數;規範中一個10 行代碼的小片段與其他部分相互作用會比100 行代碼的函數更複雜,否則就會被視為一個黑盒。
然而,這種偏好封裝複雜性的方法存在局限性。任何一段代碼中都可能出現軟件bugs,當代碼越來越大時,出現錯誤的概率接近1。有時,當你需要以意想不到的新方式與子系統交互時,最初的封裝複雜性可能會變成系統複雜性。
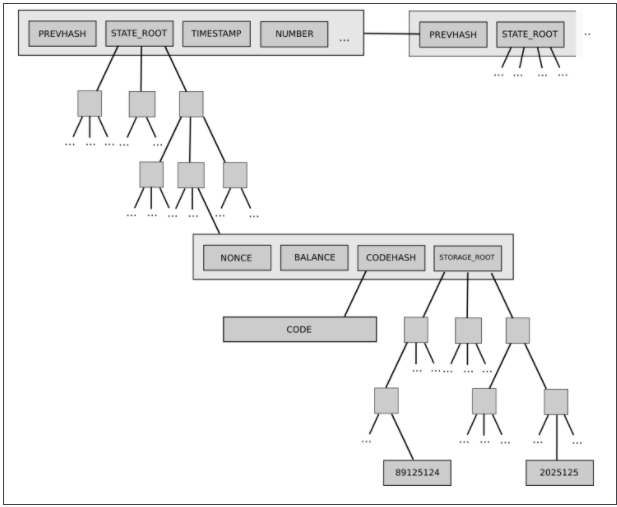
後者的一個例子是以太坊當前的兩級狀態樹(two-level state tree),其特徵是帳戶對象樹,其中每個帳戶對象依次有自己的存儲樹。這個樹結構是複雜的,但在一開始,這種複雜性似乎被很好地封裝:協議的其餘部分作為可讀寫的鍵/值存儲與樹交互,所以我們不必擔心樹是如何構造的。然而,後來,這種複雜性被證明具有系統性影響:帳戶擁有任意大的存儲樹的能力意味著沒有辦法可靠地期望某個特定的狀態部分(例如。“所有以0x1234 開頭的帳戶”) 具有可預測的大小。這使得將狀態分割成多個部分變得更加困難,使同步協議的設計和分佈存儲進程的嘗試變得更加複雜。
為什麼封裝複雜性會變成系統性的?因為interface 改變了。解決方法是什麼?目前轉向Verkle 樹的提議還包括轉向一個均衡的單層樹設計。最終,在任何給定的情況下,哪種類型的複雜性更受歡迎是一個沒有簡單答案的問題。





