原文標題：《乾貨| Schnorr 簽名如何提升比特幣》，作者Stepan

在閱讀Blockstream 撰寫的MuSig 論文時，我一直在想像，這對於我一個比特幣用戶來說，到底意味著什麼。我發現Schnorr 簽名的一些特性實在是非常棒而且便利，但某一些特性則非常煩人。在這篇文章裡，我希望能跟各位分享我的想法。不過，我們先快速回顧一下。

橢圓曲線簽名算法

當前比特幣的所有權體系用的是ECDSA（橢圓曲線簽名算法）。在簽名一條消息m 時，我們先哈希這條消息，得出一個哈希值，即z = hash(m) 。我們也需要一個隨機數（或者至少看似隨機的數）k 。在這裡，我們不希望信任隨機數生成器（有太多的錯誤和漏洞都與不合格的隨機數生成器有關），所以我們通常使用RFC6979，基於我們所知的一個秘密值和我們要簽名的消息，計算出一個確定性的k。

圖片描述

圖片描述

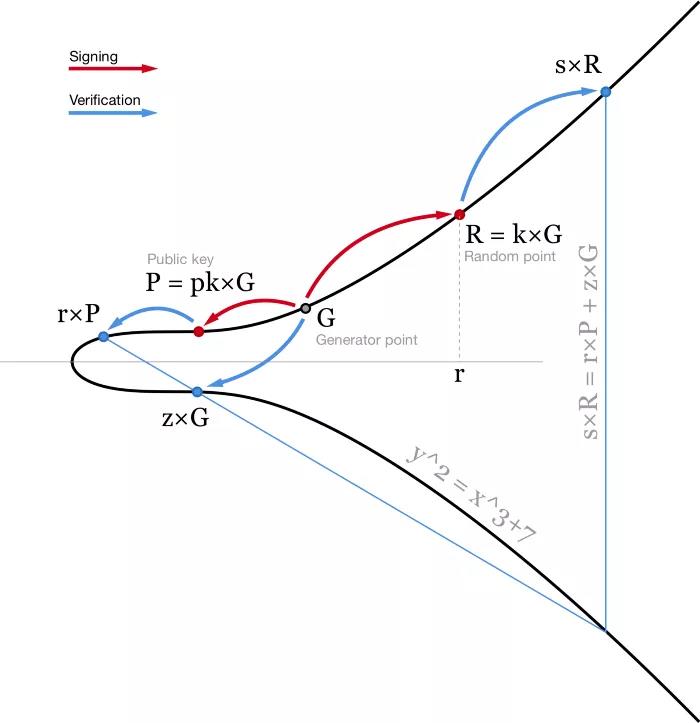
- ECDSA 算法圖解。為便於說明，橢圓曲線作在實數域上 -

圖片描述

Schnorr 簽名

Schnorr 簽名

圖片描述

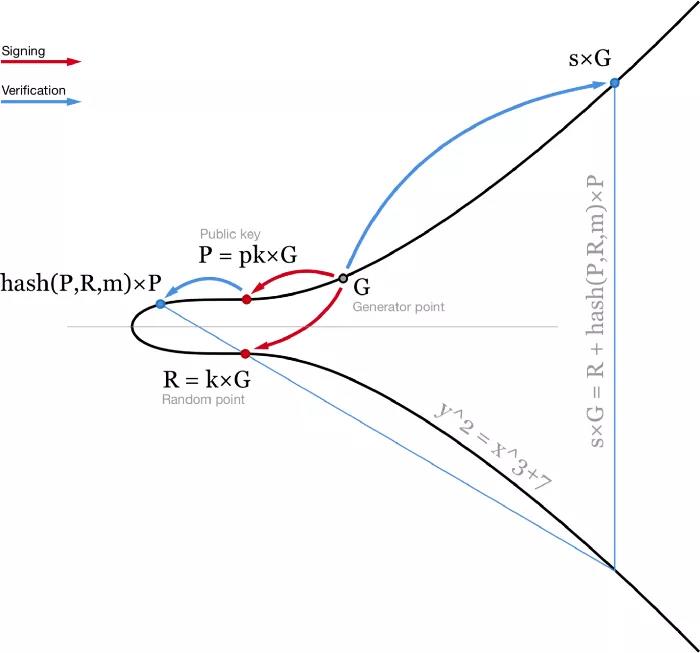
- 圖解Schnorr 簽名和驗證 -

這個等式是線性的，所以多個等式可以相加相減而等號仍然成立。這給我們帶來了Schnorr 簽名的多種良好特性。

1. 批量驗證

在驗證區塊鏈上的一個區塊時，我們需要驗證區塊中所有交易的簽名都是有效的。如果其中一個是無效的，無論是哪一個—— 我們都必須拒絕掉整個區塊。

ECDSA 的每一個簽名都必須專門驗證，意味著如果一個區塊中包含1000 條簽名，那我們就需要計算1000 次除法和2000 次點乘法，總計約3000 次繁重的運算。

圖片描述

(s1+s2+…+s1000) × G=(R1+…+R1000)+(hash(P1,R1,m1)×P1+ hash(P2,R2,m2)×P2+…+hash(P1000,R1000,m1000)×P1000)

圖片描述

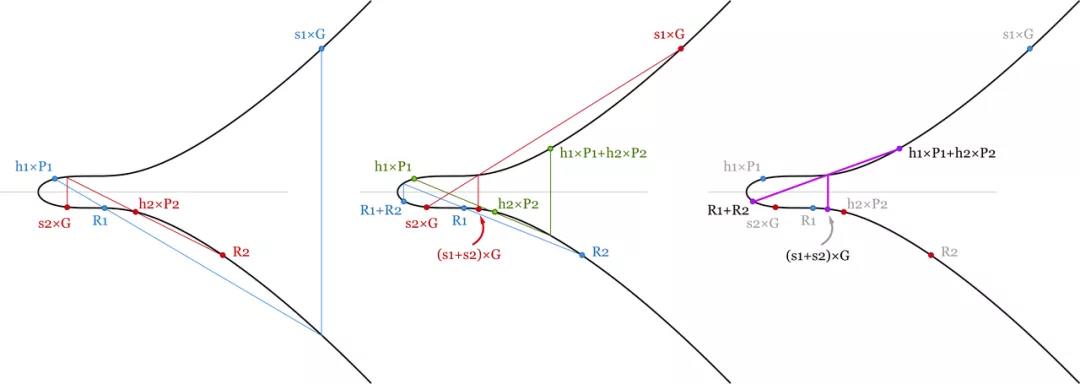
- 兩個簽名的批量驗證。因為驗證等式是線性可加的，所以只要所有的簽名都是有效的，這幾個等式的和等式也必成立。我們節約了一些運算量，因為標量和點加法比點乘法容易計算得多。 -

2. 密鑰生成

我們想要安全地保管自己的比特幣，所以我們可能會希望使用至少兩把不同的私鑰來控制比特幣。一個在筆記本電腦或者手機（在線錢包，熱錢包）上使用，而另一個放在硬件錢包/冷錢包裡面。即使其中一個洩露了，我們還是掌控著自己的比特幣。

當前，實現這種錢包的做法是通過2-2 的多簽名腳本。也就是一筆交易需要包含兩個獨立的簽名。

有了Schnorr 簽名，我們可以使用一對密鑰(pk1,pk2)，並使用一個共享公鑰P = P1 + P2 = pk1 * G + pk2 * G 生成一個共同簽名。在生成簽名時，我們需要在兩個設備上分別生成一個隨機數（k1, k2），並以此生成兩個隨機點Ri = ki * G，再分別加上hash(P, R1 + R2, m )，就可以獲得s1 和s2 了（因為si = ki + hash(P, R, m)* pki ）。最後，把它們都加起來即可獲得簽名(R, s) = (R1+R2, s1+s2)，這就是我們的共享簽名，可用共享公鑰來驗證。其他人根本無法看出這是不是一個聚合簽名，它跟一個普通的Schnorr 簽名看起來沒有兩樣。

不過，這種做法有三個問題。

第一個問題是UI 上的。要發起一筆交易，我們需要在兩個設備上發起多輪交互—— 為了計算共同的R，為了簽名。在兩把私鑰的情況下，只需訪問一次冷錢包：我們可以在熱錢包裡準備好待簽名的交易，選好k1 並生成R1 = k1 * G，然後把待簽名的交易和這些數據一同傳入冷錢包並簽名。因為已經有了R1，簽名交易在冷錢包中只需一輪就可以完成。從冷錢包中我們得到R2 和s2，傳回給熱錢包。熱錢包使用前述的（k1，R1） 簽名交易，把兩個簽名加總起來即可向外廣播交易了。

這在體驗上跟我們現在能做到的沒有什麼區別，而且每當你加多一把私鑰，問題就會變得更加複雜。假設你有一筆財富是用10 把私鑰共同控制的，而10 把私鑰分別存放在世界各地，這時候你要發送交易，該有多麻煩！在當前的ECDSA 算法中，每個設備你都只需要訪問一次，但如果你用上Schnorr 的密鑰聚合，則需要兩次，以獲得所有的Ri 並簽名。在這種情況下，可能不使用聚合，而使用各私鑰單獨簽名的方式會好一些—— 這樣就只需要一輪交互。

文章完成後，我得到了Manu Drijvers 的反饋：在一個可證明安全性的多簽名方案中，你需要3 輪交互：

• 簽名

• 簽名

• 簽名

第二個問題是已知的Rogue 密鑰攻擊。這篇論文講解得非常好，所以我就不贅述了。大概意思是如果你的其中一個設備被黑（比如你的熱錢包被劫持），並假裝自己的公鑰是（P1 - P2），那就可以僅憑私鑰pk1 便控制兩個私鑰共享的資金。一個簡單的解決方案是，在設置設備時，要求使用私鑰對相應的公鑰簽名。

還有第三個重大問題。你沒法使用確定性的k 來簽名。如果你使用了確定性的k，則只需一種簡單的攻擊，黑客即可獲得你的私鑰。攻擊如下：某個黑客黑入你的筆記本電腦，完全控制了其中一把私鑰（比如pk1）。我們感覺資金仍是安全的，因為使用我們的比特幣需要pk1 和pk2 的聚合簽名。所以我們像往常一樣發起交易，準備好一筆待簽名的交易和R1，發送給我們的硬件錢包，硬件錢包簽名後將（R2, s2）發回給熱錢包…… 然後，熱錢包出錯了，沒法完成簽名和廣播。於是我們再試一次，但這一次被黑的電腦用了另一個隨機數—— R1' 。我們在硬件錢包裡簽名了同一筆交易，又將（R2, s2'）發回給了被黑的電腦。這一次，沒有下文了—— 我們所有的比特幣都不翼而飛了。

在這次攻擊中，黑客獲得了同一筆交易的兩個有效的簽名：（R1, s1, R2, s2） 和（R1', s1'，R2，s2'）。這個R2 是一樣的，但是R = R1 + R2 和R' = R1' + R2 是不同的。這就意味著黑客可以計算出我們的第二個私鑰：s2-s2'=(hash(P,R1+R2,m)-hash(P,R1'+R2,m))⋅pk2 或者說pk2 =(s2-s2')/(hash(P,R1+R2,m)-hash(P,R1'+R2,m))。我發現這就是密鑰聚合最不方便的地方—— 我們每次都要使用一個好的隨機數生成器，這樣才能安全地聚合。

3. Musig

MuSig 解決了其中一個問題—— rogue key 攻擊將不能再奏效。這裡的目標是把多方/多個設置的簽名和公鑰聚合在一起，但又無需你證明自己具有與這些公鑰相對應的私鑰。

聚合簽名對應著聚合公鑰。但在MuSig 中，我們不是把所有聯合簽名者的公鑰直接相加，而是都乘以一些參數，使得聚合公鑰P = hash(L,P1)×P1 + … + hash(L,Pn) ×Pn 。在這裡，L = hash(P1,…,Pn) —— 這個公共數基於所有的公鑰。 L 的非線性特性阻止了攻擊者構造特殊的公鑰來發動攻擊。即使攻擊者知道他的hash(L,Patk)×Patk 應該是什麼，他也無法從中推導出Patk 來—— 這就跟你想從公鑰中推導出私鑰是一樣的。

簽名構造的其它過程跟上面介紹的很像。在生成簽名時，每個聯合簽名者都選擇一個隨機數ki 並與他人分享Ri = ki * G。然後他們把所有的隨機點加起來獲得R=R1+…+Rn ，然後生成簽名si = ki + hash(P,R,m) ⋅ hash(L,Pi) ⋅ pki 。因此，聚合簽名是(R, s)=(R1+…+Rn, s1+…+sn) ，而驗證簽名的方法與以前一樣：s×G = R + hash(P,R,m)×P 。

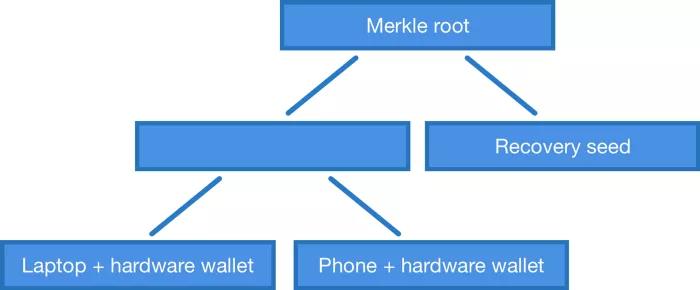
4. 默克爾樹多簽名

你可能也注意到了，MuSig 和密鑰聚合需要*所有簽名者簽名一個交易*。但如果你想做的是2-3 的多簽名腳本呢？這時候我們能夠使用簽名聚合嗎，還是不得不使用通常的OP_CHECKMULTISIG 和分別簽名？ （譯者註：OP_CHECKMULTISIG 是比特幣驗證橢圓曲線多簽名腳本的操作碼）

先說答案，是可以的，但是協議上將有些許的不同。我們可以開發一個類似於OP_CHECKMULTISIG 的操作碼，只不過是檢查聚合簽名是否對應於公鑰默克爾樹上的一個元素。

正文

正文

結論

結論

Schnorr 簽名很棒，它解決了區塊驗證中的一些計算開銷問題，也給了我們密鑰聚合的能力。後者在使用時有些不便利，但我們不是在強迫大家使用它—— 無論如何，我們都可以仍舊使用普通的多簽名方案，使用單獨的、不聚合的簽名。

（完）

（完）

（完）