一個有效的市場包含巨量信息，這些信息承載了市場對價格的判斷。但是鏈上計算資源有限，要在鏈上實現一個高度靈活的市場，就好像要把大象塞進冰箱。

把大象塞冰箱這種事情並不罕見，互聯網歷史上已經有過幾次壯舉。例如圖像壓縮，音頻壓縮。

壓縮的本質是提取最重要的特徵，拋棄不重要的細節信息。

那麼，一個市場最重要的特徵是什麼，是流動性。流動性可以表示為一張深度圖。

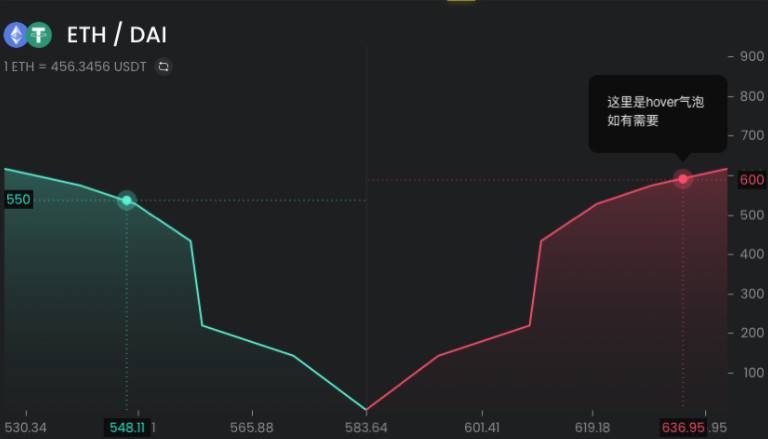
從下圖我們看到，深度圖可以抽象為兩個三角形，而描述這兩個三角形，只需要中間價和斜率即可。

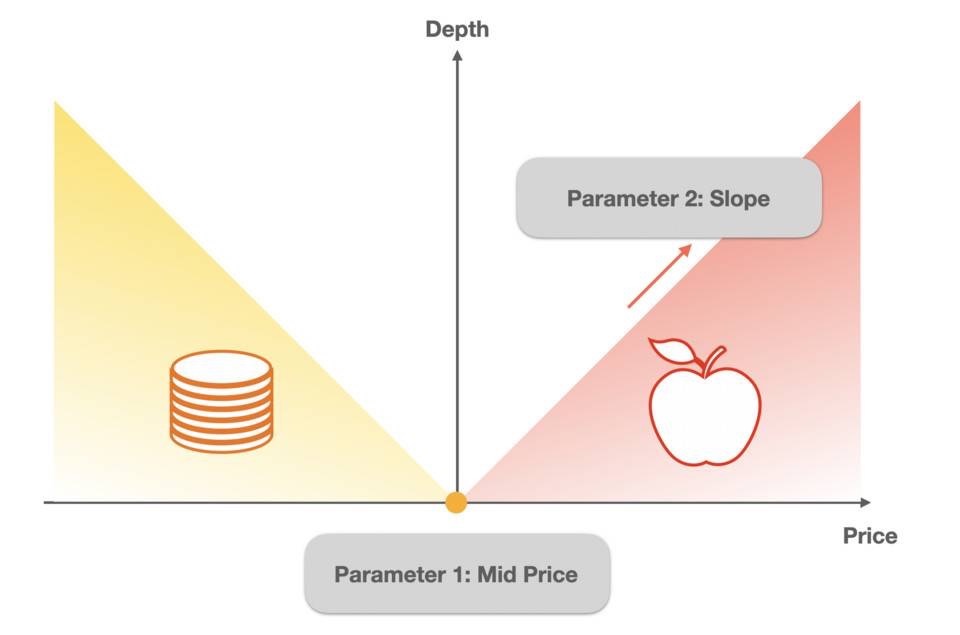
我們盯住右邊的賣盤梯形深度，它的最大特點是，被買走的Base Token 越多，價格越高。因此，這種線性深度可以表示為

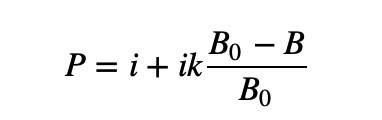
其中i 是第一個參數「mid price」，k 是第二個參數「slope」。

B 表示當前的Base Token 庫存，B0 表示初始Base Token 庫存，(B0-B)/B0 用來表示有百分之多少的BaseToken 被消耗掉了。

這一公式可以使得價格隨著Base Token 被賣出的數量線性增長。

但是，線性真的是描述流動性最好的方法嗎？並不是，線性描述有兩個局限：

1.真正的市場，大部分流動性集中市場中間價附近，而線性描述並沒有反應這種不平衡的分佈。

2.即使價格遠遠偏離市場中間價，也應該有流動性，而線性描述下的價格是有上下限的。

我們為價格曲線引入了非線性。在不擴充參數的前提下，使深度分佈更符合市場規律，靈活度更高。

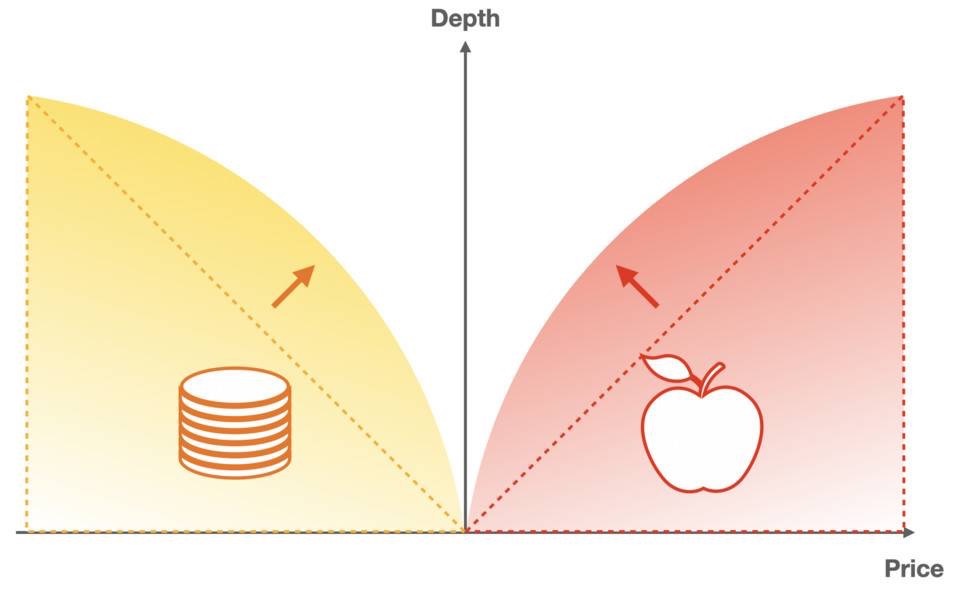
最簡單的非線性解決方案，就是使用乘法而非加法。

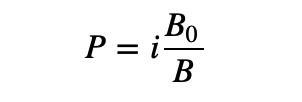
這個公式可以滿足隨著B 的減小，P 不斷增大，直至無窮大。但是要怎麼把斜率的影響加進去呢？

這就需要對B0/B 這一項做改造了。 B0/B≥1，我們用一個參數對其進行縮放，在保持此數值大於等於1 的同時，可以控制它「大於1 的程度」。

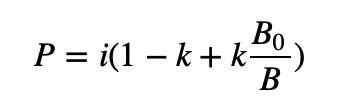
上式中，k 的取值範圍是[0,1]，決定了價格的斜率。

• 當k=0 時，價格完全不變

• 當k=1 時，價格斜率退化到上一個版本的公式

• k 越大，價格變化越敏感。 k 越小，價格變化越不敏感。

但是還有一個小問題，這裡的P 是邊際價格，對邊際價格的積分才是用戶需要支付的資產數量。上式中，B0/B 這項積分後出現了對數函數，這會使後續計算變得很複雜。為了避免這一麻煩，我們再進一步：

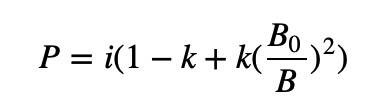
在B0/B 外面加一個平方項，這樣積分後就變成了一個簡單的除法。

令人驚嘆的是，當k=1 時，這條曲線正是AMM 所定義的bonding curve。這種巧合使我們相信，這是一套更加觸及市場本質的算法。

同理，對於左半邊的深度圖，我們用對稱的做法，將base token 替換為quote token，將乘法替換為除法：

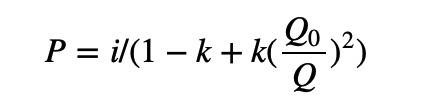
我們將左右兩邊的深度圖結合起來，就得到了PMM 算法的完全版本，整理一下：

PMM 算法是對Orderbook 市場的高度壓縮，參數簡單，卻極度靈活。

這使得我們在冰箱如此狹小的空間內，擁有了堪比大象的能力。

下面我來列舉，通過調整參數和充提規則，這套算法可以實現哪些use case。

Use Case 1 跟隨外部市場價格的主動做市

這一use case 的應用場景是擁有巨大外部市場的主流幣，例如ETH BTC 等

PMM 可以實現主動調整盤口價格，減少IL。獲得比AMM 更高的資金利用率，並且持有單幣種就能提供流動性

設置如下：

• 將價格i 設置為外部市場價格

• 將k 設置為小於1 的數字

• 允許任何人單邊充提

這一Use Case 我們稱之為DODO Classic Pool。

Use Case 2 輕資本需求的自動做市算法

這一use case 應用於沒有主觀定價能力的長尾幣市場，將定價權完全交給taker

通常來講，長尾幣都是新資產，在AMM 框架下沒有足夠的賣盤流動性，因而導致其流動性長期匱乏

設置如下：

• 將價格i 設置成起始發行價

• 任意設置 k

• 第一筆充值可以以任意資產比例，且不改變市場價

• 後續充值（或提現）必須按照當前資產比例同時操作兩種資產

Use Case 3 完全自由的做市算法

Use Case 3 完全自由的做市算法

例如：

例如：

例如：

• 在ETH=700USDT 附近做市，使用很小的k 獲得非常有競爭力的流動性，並賺取大量手續費。當察覺到ETH 有上漲預期時，撤出ETH 庫存以減少單邊風險。但這一操作並不削弱買盤流動性。

• 新資產發行項目方只提供代幣而不提供資金。在1$ 開始銷售代幣。為了讓更多人以合理價格買到代幣，設置了較小的k，使得代幣上漲溫和。隨後項目方發現需要使用資金，則可以直接提出資金池中的資產，而不損害賣盤流動性，即用戶仍然可以買到大量廉價代幣。

設置如下：

• 只有做市商能充提，允許單幣種操作

這一Use Case 我們稱之為DODO Private Pool。

Use Case 4 流動性眾籌

我們可以將新資產發行分為兩階段：

1.不開啟現貨交易，所有參與發售的人都以相同的價格獲得代幣

2.以上一階段的結束價格開啟現貨交易，使用上一階段剩餘的代幣和資產建立DODO Vending Machine

這一Use Case 我們稱之為CrowdPooling。

Use Case 5 退化為AMM

當滿足以下條件時，PPM 算法表現和AMM 相同。

• 設置k=1

• 必須按照當前價格比例同時充提兩種資產

這也意味著，AMM 是PMM 的一種特殊情況。推導過程如下：

AMM 的價格公式是xy = k，其中k 是常數，x、y 則分別代表兩種代幣的數量。為了避免字母上的歧義，我們把AMM 公式中的恆定乘積定義為Const，並將其改寫為y=Const/x。

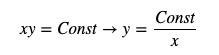
其中y 代表quote token 庫存，x 代表base token 庫存，價格可以寫為對y 求導（注意這裡要加絕對值，因為價格是正數）。

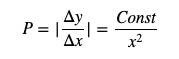
接下來回到k=1 的PMM 公式，我們可以將其寫成：

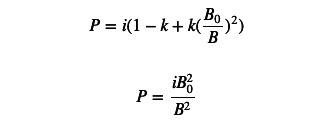
我們發現，PMM 價格公式的分子上為常數，分母為base token 的庫存。只要令

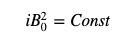
AMM 的定價公式，與PMM 的定價公式就一致了！

Use Case 6 穩定幣交易

設置如下：

• i=1

• k=0.001 （這個值越小，越接近穩定幣剛性兌換）

算法表現可以與curve 相同，並且更靈活，可以比curve 更接近剛性兌換，或更接近AMM。

撰文：雷達熊，DODO 創始人