本文作者:p0n1@安比實驗室
libsnark 是目前實現zk-SNARKs 電路最重要的框架,在眾多私密交易或隱私計算相關項目間廣泛應用,其中最著名當然要數Zcash。 Zcash 在Sapling 版本升級前一直使用libsnark 來實現電路(之後才替換為bellman)。毫不誇張地說,libsnark 支撐並促進了zk-SNARKs 技術的首次大規模應用,填補了零知識證明技術從最新理論到工程實現間的空缺。
希望通過本系列文章,所有開發者都能親自上手實踐,在短時間內迅速入門libsnark,一步步了解libsnark 的基本概念,學會如何開發zk-SNARKs 電路,完成證明的生成和驗證,最終將零知識證明應用到真實業務中去。
1. zk-SNARKs 和libsnark 背景簡介
零知識證明,可能是目前最具應用前景和想像力的密碼學黑科技。而zk-SNARKs 正是一類零知識證明方案的簡稱,全稱為Zero-Knowledge Succinct Non-interactive Arguments of Knowledge。這一名字幾乎包含了其所有技術特徵,即可以在不洩露任何其他信息的前提下證明一個命題的正確性,並且最終生成的證明具有簡潔性(Succinct),也就是說最終生成的證明足夠小,並且與計算量大小無關,是一個常數。用白話說就是,你理論上可以在不暴露任何隱私的情況下向其他所有人證明某件事,並且生成的證明體積很小,校驗成本很低,與需要證明的內容計算量無關。聽起來簡直太美好了!
zk-SNARKs 能應用到很多場景,比如隱私保護、區塊鏈擴容、可驗證計算等。本文不介紹zk-SNARKS 和零知識證明的理論細節,不熟悉或想深入了解的同學可閱讀其他文章或論文。
如Vitalik 寫的關於zk-SNARKs 著名的三篇博文。
https://medium.com/@VitalikButerin/quadratic-arithmetic-programs-from-zero-to-hero-f6d558cea649
https://medium.com/@VitalikButerin/exploring-elliptic-curve-pairings-c73c1864e627
https://medium.com/@VitalikButerin/zk-snarks-under-the-hood-b33151a013f6
或者閱讀向程@HUST寫的「深入淺出零知識證明之zk-SNARKs」,還有東澤寫的「淺談零知識證明之二:簡短無交互證明(SNARK)」。
和和和「從零開始學習zk-SNARK」系列,以及從安比實驗室維護的「零知識證明學習資源匯總」中查找更多資料。
本文主角libsnark 是用於開發zk-SNARKs 應用的C++ 代碼庫,由SCIPR Lab 開發並維護。 libsnark 工程實現背後的理論基礎是近年來(尤其是2013 年以來)零知識證明特別是zk-SNARKs 方向的一系列重要論文。如以下最著名的數篇:
[GGPR13] Quadratic span programs and succinct NIZKs without PCPs , Rosario Gennaro, Craig Gentry, Bryan Parno, Mariana Raykova, EUROCRYPT 2013
[PGHR13] Pinocchio: Nearly Practical Verifiable Computation , Bryan Parno, Craig Gentry, Jon Howell, Mariana Raykova, IEEE Symposium on Security and Privacy (Oakland) 2013
[BCGTV13] SNARKs for C: Verifying Program Executions Succinctly and in Zero Knowledge , Eli Ben-Sasson, Alessandro Chiesa, Daniel Genkin, Eran Tromer, Madars Virza, CRYPTO 2013
[BCIOP13] Succinct non-interactive arguments via linear interactive Proofs , Nir Bitansky, Alessandro Chiesa, Yuval Ishai, Rafail Ostrovsky, Omer Paneth, Theory of Cryptography Conference 2013
[BCTV14a] Succinct non-interactive zero knowledge for a von Neumann architecture , Eli Ben-Sasson, Alessandro Chiesa, Eran Tromer, Madars Virza, USENIX Security 2014
[BCTV14b] Scalable succinct non-interactive arguments via cycles of elliptic curves , Eli Ben-Sasson, Alessandro Chiesa, Eran Tromer, Madars Virza, CRYPTO 2014
[Groth16] On the Size of Pairing-based Non-interactive Arguments , Jens Groth, EUROCRYPT 2016
libsnark 的開發者們亦是這個領域內頂尖的學者或研究牛人,如Eran Tromer 更是以上多篇論文的共同作者。
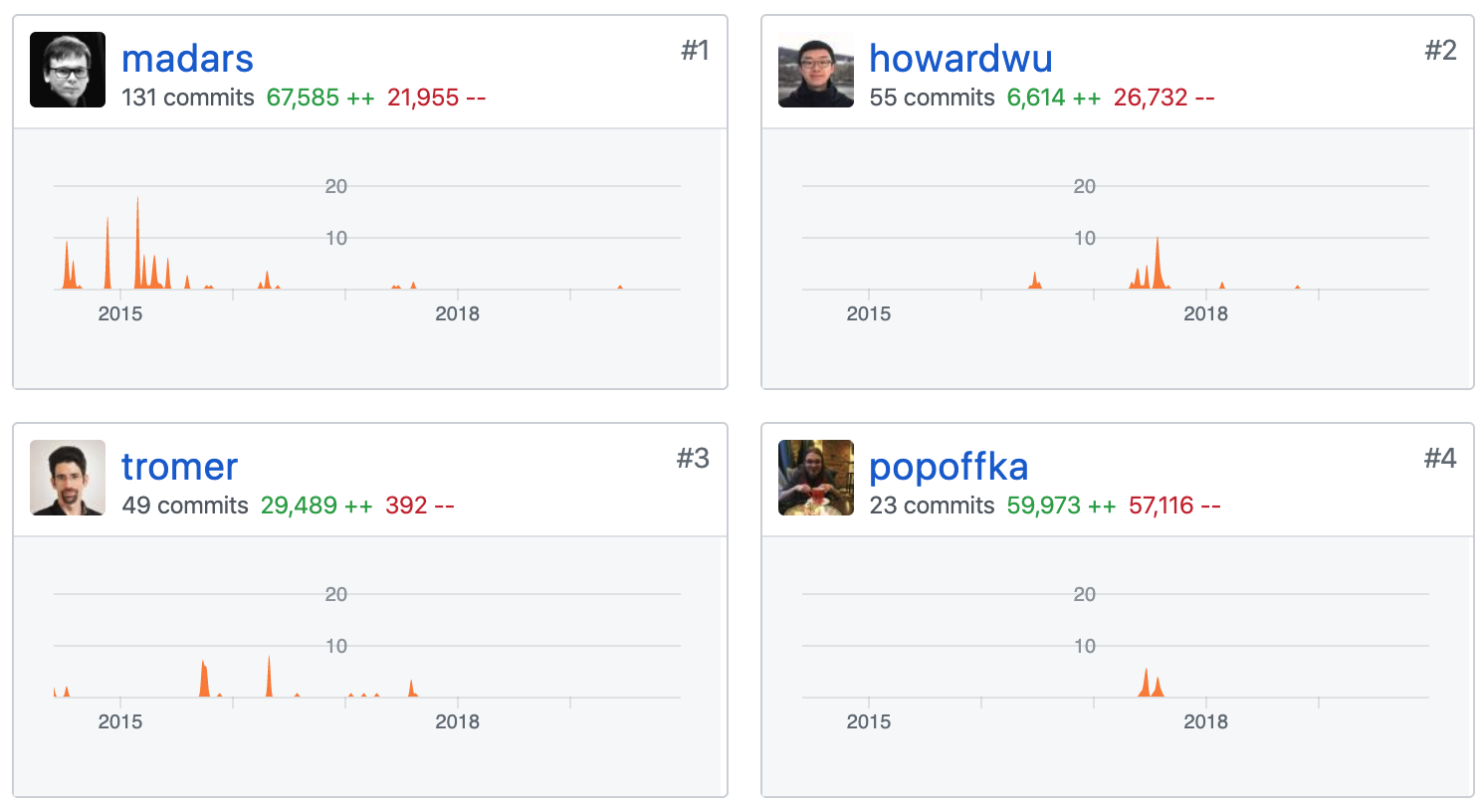
紮實的理論基礎和工程能力,讓libsnark 的作者們能夠化繁為簡,將形如下圖的高深理論和復雜公式逐一實現,高度工程化地抽像出簡潔的接口供廣大開發者方便地調用。向這些將非凡的理論研究推廣至更大規模應用的先鋒們致敬。

下圖是libsnark 的模塊總覽圖,摘自libsnark 代碼貢獻量第一作者Madars Virza 在MIT 的博士論文。
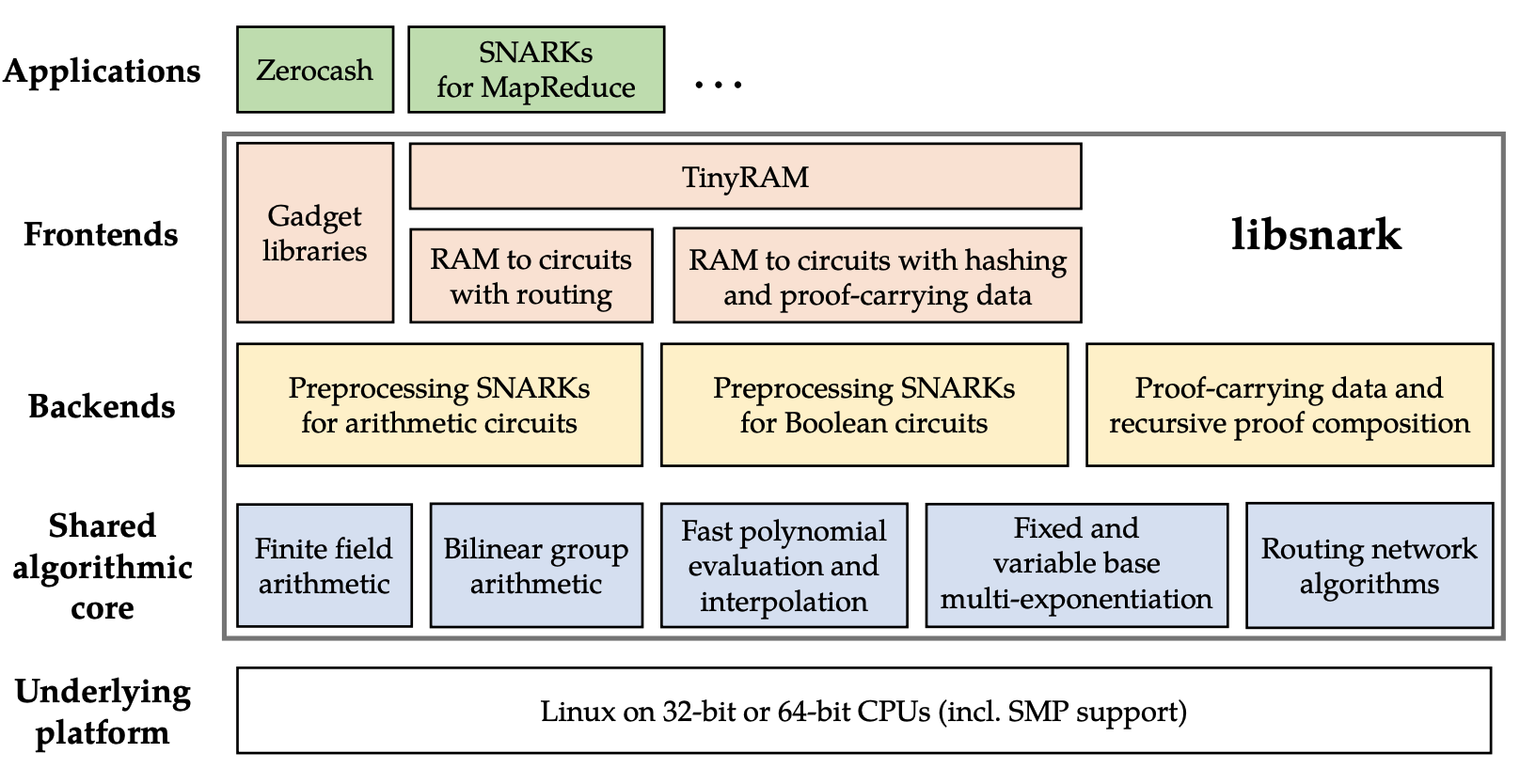
)
其中:
其中:
其中:
zk_proof_systems/ppzksnark/r1cs_ppzksnark 對應的是BCTV14a
zk_proof_systems/ppzksnark/r1cs_gg_ppzksnark 對應的是Groth16
如果想研究這兩個協議的實現細節可直接從這兩個目錄入手。 ppzksnark 是指preprocessing zkSNARK。這裡的pp/preprocessing 其實就是指我們常說的trusted setup,即在證明生成和驗證之前,需要通過一個生成算法來創建相關的公共參數(proving key 和verification key)。我們也把這個提前生成的參數稱為「公共參考串」(Common Reference String),或簡稱為CRS。
2. 基本原理與步驟
利用libsnark 庫開發zk-SNARKs 應用從原理上可簡要概括為以下四個步驟:
將待證明的命題表達為R1CS (Rank One Constraint System)
使用生成算法(G)為該命題生成公共參數
使用證明算法(P)生成R1CS 可滿足性的證明
這篇文章
這篇文章這篇文章。
有這樣一個函數C(x, out),用於判斷秘密x 是否滿足等式x^3 + x + 5 == out,若滿足則返回true。
function C(x, out) {
return ( x^3 + x + 5 == out );
}
第一步,我們需要將函數C(x, out) 在libsnark 中進行表達。此處先省略,後面介紹詳細過程。
第二步,對應下面的Generator 函數(G),lambda 為隨機產生,也就是常說的trusted setup 過程中產生的"toxic waste"。人們喜歡稱它為“有毒廢物”,是因為它必須被妥善處理(如必須銷毀,不能讓任何人知道),否則會影響證明協議安全。
lambda <- random()
(pk, vk) = G(C, lambda)
最終生成proving key (pk) 和verification key (vk)。
第三步,對應使用Prove 函數(P)生成證明。這裡想證明的是prover 知道一個秘密值x 和計算結果out 可使等式滿足。因此將x、out 還有pk 作為輸入一起傳給P,最終生成證明proof。
proof = P(pk, out, x)
第四步,對應使用Verify 函數(V)驗證證明,將proof、out 還有vk 傳給G,即可在不暴露秘密的情況下證明存在一個秘密值可使等式滿足。
V(vk, out, proof) ?= true
而開發者主要工作量就集中在第一步,需要按照libsnark 的接口規則手寫C++ 電路代碼來描述命題,由代碼構造R1CS 約束。整個過程也即對應下圖的Computation -> Arithmetic Circuit -> R1CS。

3. 搭建zk-SNARKs 應用開發環境
下面進入動手環節,快速上手libsnark,跑通例子。
先下載本文對應的libsnark 最小可用例子代碼庫libsnark_abc。
git clone https://github.com/sec-bit/libsnark_abc.git
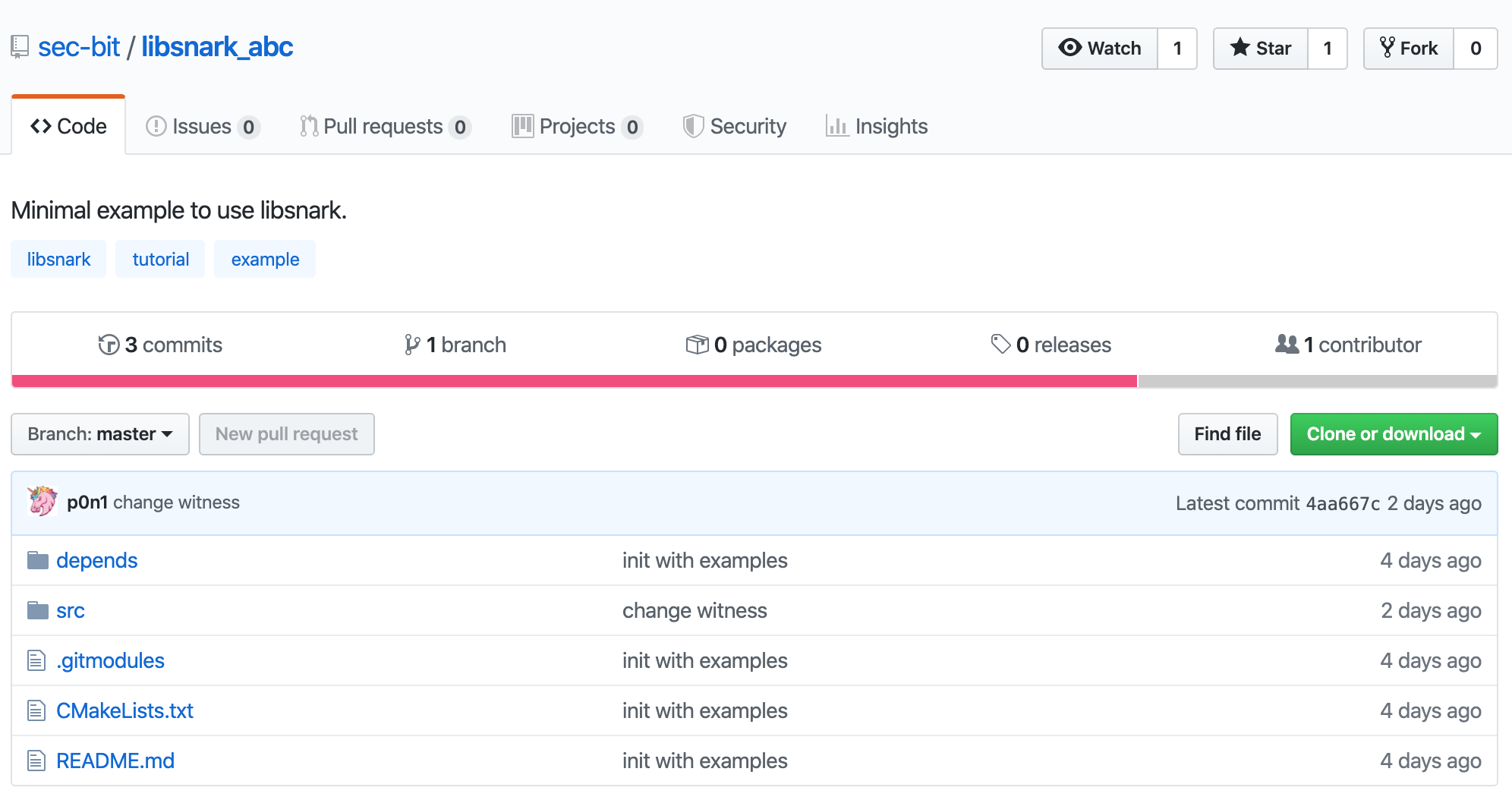
通過git submodule 拉取libsnark 代碼。
cd libsnark_abc
git submodule update --init --recursive
參考libsnark項目文檔完成相關依賴安裝。以Ubuntu 16.04 LTS 為例,需安裝以下組件:
sudo apt-get install build-essential cmake git libgmp3-dev libprocps4-dev python-markdown libboost-all-dev libssl-dev
初始化build 文件夾。
mkdir build && cd build && cmake ..
這步在macOS 系統可能會遇到問題,參考這個issue處理。或嘗試使用以下命令:
mkdir build && cd build && CPPFLAGS=-I/usr/local/opt/openssl/include LDFLAGS=-L/usr/local/opt/openssl/lib PKG_CONFIG_PATH=/usr/local/opt/openssl/lib/pkgconfig cmake -DWITH_PROCPS=OFF -DWITH_SUPERCOP=OFF ..
成功後,依舊在build 目錄進行編譯。
make
編譯成功後,在build/src 目錄中可看到3 個二進製文件。
main
range
test
到這兒,你就以及完成示例項目的編譯啦。嘗試運行示例代碼吧。
./src/main
最終出現如下日誌,則說明一切正常。你已順利擁有了zkSNARK 應用開發環境,並成功跑了第一個zk-SNARKs 的demo。
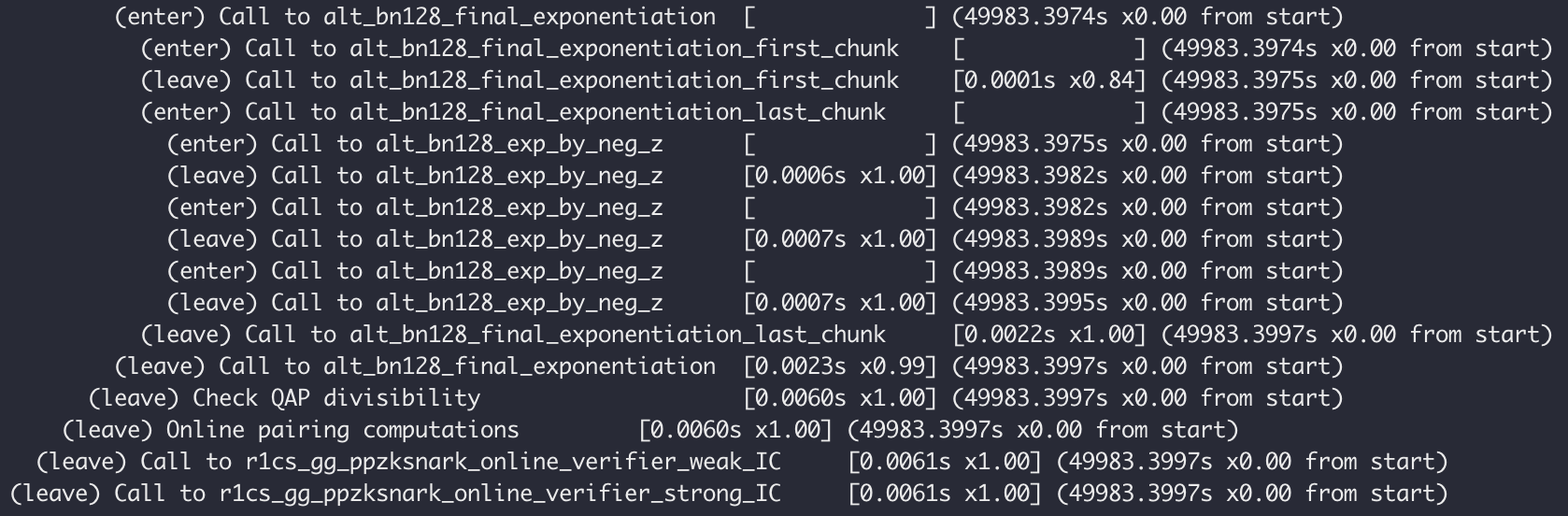
4. 理解示例代碼
下面我們一起來仔細瞅瞅代碼。示例項目包含了3 份代碼(也可查看文末附錄)。
不妨先看看src/main.cpp。這個例子來自Howard Wu 的libsnark_tutorial,他也是libsnark 作者之一哦。本文libsnark_abc 的項目結構就是依照他的libsnark_tutorial 搭建,屬於“官方推薦風格” ,請放心食用😆。
只有區區幾十行代碼,其中run_r1cs_gg_ppzksnark() 是主要部分。很容易發現,真正起作用的實質代碼只有下面5 行。
r1cs_gg_ppzksnark_keypair
r1cs_gg_ppzksnark_processed_verification_key
r1cs_gg_ppzksnark_proof
const bool ans = r1cs_gg_ppzksnark_verifier_strong_IC
const bool ans2 = r1cs_gg_ppzksnark_online_verifier_strong_IC
僅從“超長”的函數名就能看出來每步是在做什麼,但是卻看不到如何構造電路的細節。實際上這裡僅僅是調用了自帶的r1cs_example,隱去了實現細節。
既然如此,那讓我們通過一個更直觀的例子來學習電路細節。研究src/test.cpp,這個例子改編自Christian Lundkvist 的libsnark-tutorial。
代碼開頭僅引用了三個頭文件,分別是:
#include
#include
#include
前面提到r1cs_gg_ppzksnark 對應的是Groth16 方案。這裡加了gg 是為了區別r1cs_ppzksnark(也就是BCTV14a 方案),表示Generic Group Model(通用群模型)。 Groth16 安全性證明依賴Generic Group Model,以更強的安全假設換得了更好的性能和更短的證明。
第一個頭文件是為了引入default_r1cs_gg_ppzksnark_pp 類型,第二個則為了引入證明相關的各個接口。 pb_variable 則是用來定義電路相關的變量。
下面需要進行一些初始化,定義使用的有限域,並初始化曲線參數。這是相當於每次的準備工作。
typedef libff::Fr
default_r1cs_gg_ppzksnark_pp::init_public_params();
接下來就需要明確「待證命題」是什麼。這裡不妨沿用之前的例子,證明秘密x 滿足等式x^3 + x + 5 == out。這實際也是Vitalik 博文"Quadratic Arithmetic Programs: from Zero to Hero"中用的例子。如果對下面的變化陌生,可嘗試閱讀該博文。
通過引入中間變量sym_1、y、sym_2 將x^3 + x + 5 = out 扁平化為若干個二次方程式,幾個只涉及簡單乘法或加法的式子,對應到算術電路中就是乘法門和加法門。你可以很容易地在紙上畫出對應的電路。
x * x = sym_1
sym_1 * x = y
y + x = sym_2
sym_2 + 5 = out
通常文章到這里便會順著介紹如何按照R1CS 的形式編排上面的幾個等式,並一步步推導出具體對應的向量。這對理解如何把Gate 轉換為R1CS 有幫助,然而卻不是本文的核心目的。所以此處省略一百字。
下面定義與命題相關的變量。首先創建的protoboard 是libsnark 中的一個重要概念,顧名思義就是原型板或者麵包板,用來快速搭建電路,在zk-SNARKs 電路中則是用來關聯所有變量、組件和約束。接下來的代碼定義了所有需要外部輸入的變量以及中間變量。
// Create protoboard
protoboard
// Define variables
pb_variable
pb_variable
pb_variable
pb_variable
pb_variable
下面將各個變量與protoboard 連接,相當於把各個元器件插到“麵包板”上。 allocate() 函數的第二個string 類型變量僅是用來方便DEBUG 時的註釋,方便DEBUG 時查看日誌。
out.allocate(pb, "out");
x.allocate(pb, "x");
sym_1.allocate(pb, "sym_1");
y.allocate(pb, "y");
sym_2.allocate(pb, "sym_2");
pb.set_input_sizes(1);
注意,此處第一個與pb 連接的是out 變量。我們知道zk-SNARKs 中有public input 和private witness 的概念,分別對應libsnark 中的primary 和auxiliary 變量。那麼如何在代碼中進行區分呢?我們需要藉助set_input_sizes(n) 來聲明與protoboard 連接的public/primary 變量的個數n。在這裡n = 1,表明與pb 連接的前n = 1 個變量是public 的,其餘都是private 的。
至此, 所有變量都已經順利與protoboard 相連,下面需要確定的是這些變量間的約束關係。這個也很好理解,類似元器件插至麵包板後,需要根據電路需求確定他們之間的關係再連線焊接。如下調用protoboard 的add_r1cs_constraint() 函數,為pb 添加形如a * b = c 的r1cs_constraint。即r1cs_constraint
// x*x = sym_1
pb.add_r1cs_constraint(r1cs_constraint
// sym_1 * x = y
pb.add_r1cs_constraint(r1cs_constraint
// y + x = sym_2
pb.add_r1cs_constraint(r1cs_constraint
// sym_2 + 5 = ~out
pb.add_r1cs_constraint(r1cs_constraint
至此,變量間的約束也已添加完成,針對命題的電路已構建完畢。下面進入前文提到的“四個步驟”中的第二步:使用生成算法(G)為該命題生成公共參數(pk 和vk),即trusted setup。生成出來的proving key 和verification key 分別可以通過keypair.pk 和keypair.vk 獲得。
const r1cs_constraint_system
const r1cs_gg_ppzksnark_keypair
進入第三步,生成證明。先為public input 以及witness 提供具體數值。不難發現,x = 3, out = 35 是原始方程的一個解。則依次為x、out 以及各個中間變量賦值。
pb.val(out) = 35;
pb.val(x) = 3;
pb.val(sym_1) = 9;
pb.val(y) = 27;
pb.val(sym_2) = 30;
再把public input 以及witness 的數值傳給prover 函數進行證明,可分別通過pb.primary_input() 和pb.auxiliary_input() 訪問。生成的證明用proof 變量保存。
const r1cs_gg_ppzksnark_proof
最後我們使用verifier 函數校驗證明。如果verified = true 則說明證明驗證成功。
bool verified = r1cs_gg_ppzksnark_verifier_strong_IC
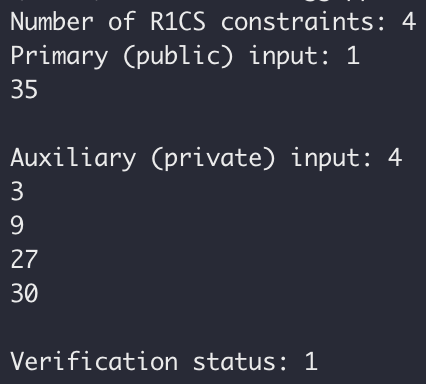
從日誌輸出中可以看出驗證結果為true,R1CS 約束數量為4,public input 和private input 數量分別為1 和4。日誌輸出符合預期。
實際應用中,trusted setup、prove、verify 會由不同角色分別開展,最終實現的效果就是prover 給verifier 一段簡短的proof 和public input,verifier 可以自行校驗某命題是否成立。對於前面的例子,就是能在不知道方程的解x 具體是多少的情況下,驗證prover 知道一個秘密的x 可以使得x^3 + x + 5 = out 成立。
通過短短的幾十行代碼,你就可以很輕易地操控學術界zk-SNARKs 最新研究成果。
5. 再次上手實踐
經過上面的例子,我們已經了解了利用libsnark 庫開發zk-SNARKs 電路的所有重要步驟。
現在不妨用新的例子來鞏固一下:在不洩露秘密數字大小的前提下,證明數字小於60。
這個在常規程序裡用一個運算符就能完成的事情,在libsnark 下面應該如何表示呢?
zk-SNARKs 電路開發的主要工作量和難點在於如何用代碼“精確”地描述命題中的所有約束。一旦描述不“精確”,則要么是漏掉約束、要么是寫錯約束,最終電路想要證明的內容則會與原命題相差甚遠。上一節的例子只涉及簡單的乘法和加法,與r1cs_constraint 最基本的形式一致,因此約束的表達相對容易。除此之外幾乎所有的約束都不是很直觀,作為初學者很難正確地描述約束細節。
幸好libsnark 已經為我們實現了大量基礎電路小組件。 gadgetlib1 和gadgetlib2 下提供了許多可以直接使用的gadget。其中gadgetlib1 更常用一些,裡面收集了包括sha256 在內的hash 計算、merkle tree、pairing 等電路實現。
DangDangDang,gadgetlib1/gadgets/basic_gadgets.hpp 中的comparison_gadget 正是我們所需。
comparison_gadget(protoboard
const size_t n,
const pb_linear_combination
const pb_linear_combination
const pb_variable
const pb_variable
const std::string &annotation_prefix="")
::generate_r1cs_constraints() 研究。
這裡需要創建以下變量,並將x 和max 與pb 相連,把max 值設為60,代表數值上限。
protoboard
pb_variable
pb_variable
x.allocate(pb, "x");
max.allocate(pb, "max");
pb.val(max)= 60;
使用comparison_gadget 創建cmp,並把前面的參數填入,並調用gadget 自帶的generate_r1cs_constraints() 方法。同時另外添加一個約束,要求less * 1 = 1,也就是less 必須為true。
comparison_gadget
cmp.generate_r1cs_constraints();
pb.add_r1cs_constraint(r1cs_constraint
輸入witness(秘密值x),比如讓x = 18。這裡還需要調用comparison_gadget 的generate_r1cs_witness 方法。
// Add witness values
pb.val(x) = 18; // secret
cmp.generate_r1cs_witness();
其餘部分和上一個例子一致,即可在不洩露秘密數字大小的前提下,證明某數字小於60。同理,就實現一個對數值作最大和最小值限定的“range proof”。
在強大基礎庫的幫助下,我們又用更短的代碼實現了證明需求。
6. What's NEXT?
讀到這裡,相信大家都對libsnark 的使用方法和zk-SNARKs 電路開發有了一個初步的了解。
你或許已經發現,libsnark 的使用方法較簡單,而真正的重點在於zk-SNARKs 電路開發。正如前面提過的,必須用代碼“精確”描述待證命題中的所有約束,“漏掉”或“寫錯”約束都會讓證明內容與原本意圖大相徑庭,從而導致證明無意義。
如何正確高效地把真實業務邏輯轉化為zk-SNARKs 電路代碼,這正是我們開發者需要不斷研究和練習的。
好在我們已經有了一個libsnark 試驗場,可以很方便地自由修改、添加代碼來嘗試。
不論多複雜的電路實現,都是通過一個個更簡單地「電路組件」組合封裝而形成。因此libsnark 自帶的基礎庫是一個非常重要的學習資料——既要學習它們的使用方法,又要研究其實現原理。
我們也能通過閱讀其他項目的電路實現來了解如何將ZKP 應用到實際業務中,如HarryR 的ethsnarks-miximus和Loopring 的protocol3-circuits。從這些項目中可以學習到如何工程化地開發更大規模的電路,以及與電路性能相關的各種設計優化細節,同時對電路約束規模會有更深刻的理解。
同時也歡迎大家繼續關注安比實驗室「零知識證明Learn by Coding:libsnark 系列」後續文章,下次我們將嘗試從zk-SNARKs 與智能合約的結合、電路模塊化開發、更複雜的libsnark 實現案例、電路開發過程中容易踩的坑等角度來進一步討論。
7. 附錄
main.cpp
第一個例子main.cpp,調用libsnark 官方example 的示例代碼。通過該例子可了解libsnark 的基本使用流程和主要函數。
#include
#include
#include
#include
using namespace libsnark;
/**
* The code below provides an example of all stages of running a R1CS GG-ppzkSNARK.
*
* Of course, in a real-life scenario, we would have three distinct entities,
* mangled into one in the demonstration below. The three entities are as follows.
* (1) The "generator", which runs the ppzkSNARK generator on input a given
* constraint system CS to create a proving and a verification key for CS.
* (2) The "prover", which runs the ppzkSNARK prover on input the proving key,
* a primary input for CS, and an auxiliary input for CS.
* (3) The "verifier", which runs the ppzkSNARK verifier on input the verification key,
* a primary input for CS, and a proof.
*/
template
bool run_r1cs_gg_ppzksnark(const r1cs_example
{
libff::print_header("R1CS GG-ppzkSNARK Generator");
r1cs_gg_ppzksnark_keypair
printf("\n"); libff::print_indent(); libff::print_mem("after generator");
libff::print_header("Preprocess verification key");
r1cs_gg_ppzksnark_processed_verification_key
libff::print_header("R1CS GG-ppzkSNARK Prover");
r1cs_gg_ppzksnark_proof
printf("\n"); libff::print_indent(); libff::print_mem("after prover");
libff::print_header("R1CS GG-ppzkSNARK Verifier");
const bool ans = r1cs_gg_ppzksnark_verifier_strong_IC
printf("\n"); libff::print_indent(); libff::print_mem("after verifier");
printf("* The verification result is: %s\n", (ans ? "PASS" : "FAIL"));
libff::print_header("R1CS GG-ppzkSNARK Online Verifier");
const bool ans2 = r1cs_gg_ppzksnark_online_verifier_strong_IC
assert(ans == ans2);
return ans;
}
template
void test_r1cs_gg_ppzksnark(size_t num_constraints, size_t input_size)
{
r1cs_example
const bool bit = run_r1cs_gg_ppzksnark
assert(bit);
}
int main () {
default_r1cs_gg_ppzksnark_pp::init_public_params();
test_r1cs_gg_ppzksnark
return 0;
}
test.cpp
第二個例子test.cpp。這個例子具體展示瞭如何利用libsnark 構建一個最簡單的電路。
#include
#include
#include
using namespace libsnark;
using namespace std;
int main () {
typedef libff::Fr
// Initialize the curve parameters
default_r1cs_gg_ppzksnark_pp::init_public_params();
// Create protoboard
protoboard
// Define variables
pb_variable
pb_variable
pb_variable
pb_variable
pb_variable
// Allocate variables to protoboard
// The strings (like "x") are only for debugging purposes
out.allocate(pb, "out");
x.allocate(pb, "x");
sym_1.allocate(pb, "sym_1");
y.allocate(pb, "y");
sym_2.allocate(pb, "sym_2");
// This sets up the protoboard variables
// so that the first one (out) represents the public
// input and the rest is private input
pb.set_input_sizes(1);
// Add R1CS constraints to protoboard
// x*x = sym_1
pb.add_r1cs_constraint(r1cs_constraint
// sym_1 * x = y
pb.add_r1cs_constraint(r1cs_constraint
// y + x = sym_2
pb.add_r1cs_constraint(r1cs_constraint
// sym_2 + 5 = ~out
pb.add_r1cs_constraint(r1cs_constraint
const r1cs_constraint_system
// generate keypair
const r1cs_gg_ppzksnark_keypair
// Add public input and witness values
pb.val(out) = 35;
pb.val(x) = 3;
pb.val(sym_1) = 9;
pb.val(y) = 27;
pb.val(sym_2) = 30;
// generate proof
const r1cs_gg_ppzksnark_proof
// verify
bool verified = r1cs_gg_ppzksnark_verifier_strong_IC
cout << "Number of R1CS constraints: " << constraint_system.num_constraints() << endl;
cout << "Primary (public) input: " << pb.primary_input() << endl;
cout << "Auxiliary (private) input: " << pb.auxiliary_input() << endl;
cout << "Verification status: " << verified << endl;
}
range.cpp
第三個例子range.cpp。該例子利用了libsnark 自帶的comparison_gadget 來實現取值範圍證明。
#include
#include
#include
#include
using namespace libsnark;
using namespace std;
int main () {
typedef libff::Fr
// Initialize the curve parameters
default_r1cs_gg_ppzksnark_pp::init_public_params();
// Create protoboard
protoboard
pb_variable
pb_variable
x.allocate(pb, "x");
max.allocate(pb, "max");
pb.val(max)= 60;
comparison_gadget
cmp.generate_r1cs_constraints();
pb.add_r1cs_constraint(r1cs_constraint
const r1cs_constraint_system
// generate keypair
const r1cs_gg_ppzksnark_keypair
// Add witness values
pb.val(x) = 18; // secret
cmp.generate_r1cs_witness();
// generate proof
const r1cs_gg_ppzksnark_proof
// verify
bool verified = r1cs_gg_ppzksnark_verifier_strong_IC
cout << "Number of R1CS constraints: " << constraint_system.num_constraints() << endl;
cout << "Primary (public) input: " << pb.primary_input() << endl;
cout << "Auxiliary (private) input: " << pb.auxiliary_input() << endl;
cout << "Verification status: " << verified << endl;
}





