An efficient market contains a huge amount of information, which carries the market's judgment on prices. However, the computing resources on the chain are limited. To realize a highly flexible market on the chain is like stuffing an elephant into a refrigerator.

Stuffing elephants in refrigerators is not uncommon, and there have been several feats in the history of the internet. Such as image compression, audio compression.

The essence of compression is to extract the most important features and discard unimportant details.

So, what is the most important feature of a market is liquidity. Liquidity can be represented as a depth map.

From the figure below, we can see that the depth map can be abstracted into two triangles, and to describe these two triangles, only the median price and slope are needed.

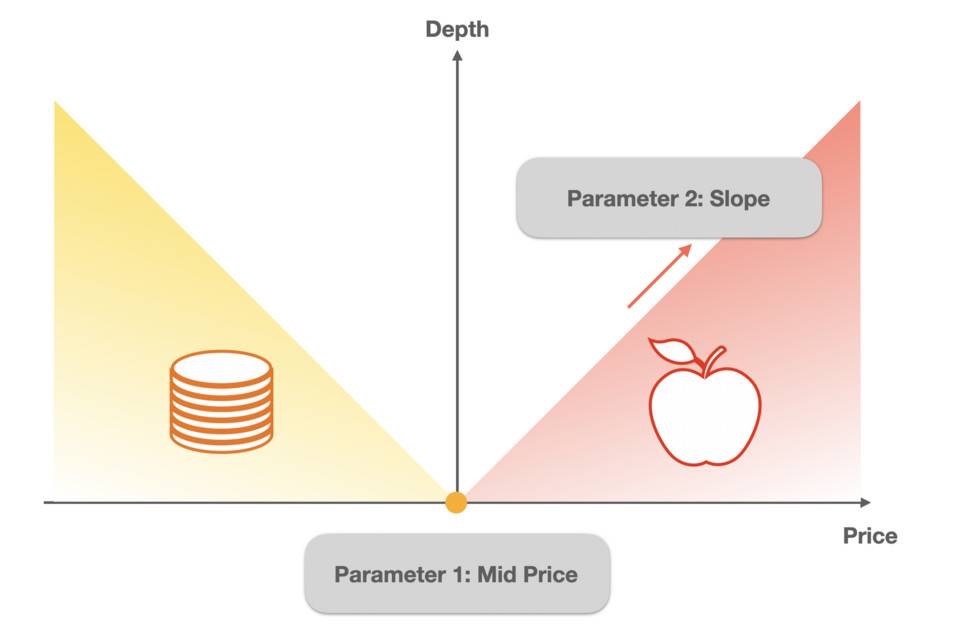
We focus on the depth of the selling trapezoid on the right. Its biggest feature is that the more Base Tokens are bought, the higher the price. Therefore, this linear depth can be expressed as

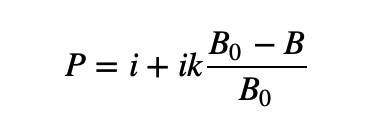
Where i is the first parameter "mid price" and k is the second parameter "slope".

B represents the current Base Token inventory, B0 represents the initial Base Token inventory, and (B0-B)/B0 is used to indicate the percentage of BaseToken consumed.

This formula can make the price increase linearly with the number of Base Token sold.

But is linear really the best way to describe mobility? No, linear description has two limitations:

1. In the real market, most of the liquidity is concentrated near the middle price of the market, and the linear description does not reflect this unbalanced distribution.

2. Even if the price deviates far from the middle price of the market, there should be liquidity, and the price under the linear description has upper and lower limits.

We introduce non-linearity to the price curve. On the premise of not expanding the parameters, the depth distribution is more in line with market rules and has higher flexibility.

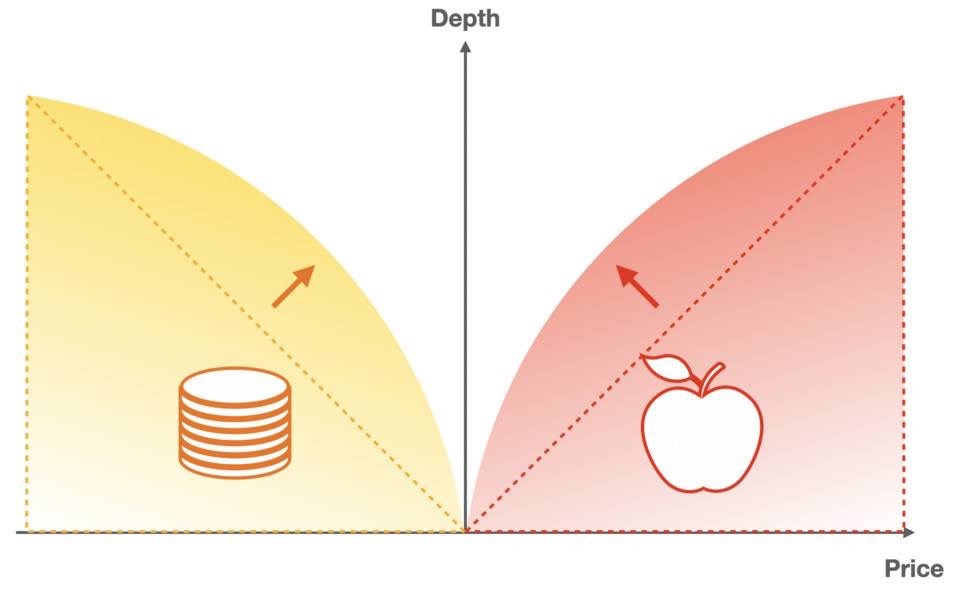
The simplest non-linear solution is to use multiplication instead of addition.

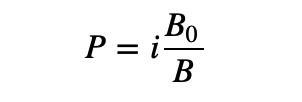
This formula can satisfy that as B decreases, P increases continuously until infinity. But how do you add the effect of the slope?

This requires a modification of the B0/B item. B0/B≥1, we use a parameter to scale it, while keeping this value greater than or equal to 1, we can control its "degree greater than 1".

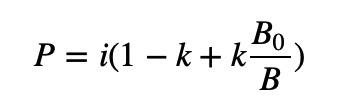
In the above formula, the value range of k is [0,1], which determines the slope of the price.

• When k=0, the price is completely unchanged

• When k=1, the price slope degenerates to the previous version of the formula

• The larger k is, the more sensitive to price changes. The smaller k is, the less sensitive to price changes.

But there is still a small problem, where P is the marginal price, and the integral to the marginal price is the amount of assets that users need to pay. In the above formula, a logarithmic function appears after the integral of B0/B, which will make subsequent calculations very complicated. To avoid this trouble, we go one step further:

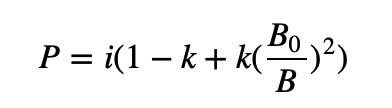
Add a square term outside B0/B so that after integration it becomes a simple division.

Surprisingly, when k=1, this curve is exactly the bonding curve defined by AMM. This coincidence makes us believe that this is a set of algorithms that touches the essence of the market more.

Similarly, for the depth map on the left half, we use a symmetrical approach to replace the base token with the quote token, and replace the multiplication with division:

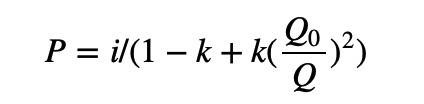
We combine the depth maps on the left and right sides to get the complete version of the PMM algorithm, sort it out:

The PMM algorithm is a highly compressed orderbook market with simple parameters but extremely flexible.

This allows us to have the power of an elephant in such a small space in the refrigerator.

Let me list the use cases that this algorithm can achieve by adjusting parameters and deposit and withdrawal rules.

Use Case 1 Active market making following external market prices

The application scenario of this use case is the mainstream currency with a huge external market, such as ETH, BTC, etc.

PMM can realize the active adjustment of handicap price and reduce IL. Obtain a higher capital utilization rate than AMM, and hold a single currency to provide liquidity

The settings are as follows:

• Set price i to the external market price

• set k to a number less than 1

• Allow anyone to deposit and withdraw unilaterally

We call this Use Case DODO Classic Pool.

Use Case 2 Automatic Market Making Algorithm for Light Capital Requirements

This use case is applied to the long-tail currency market without subjective pricing power, and the pricing power is completely handed over to the taker

Generally speaking, long-tail coins are new assets, and there is not enough selling liquidity under the AMM framework, resulting in a long-term lack of liquidity

The settings are as follows:

• Set price i as the initial issue price

• Set k arbitrarily

• The first recharge can be at any asset ratio without changing the market price

• Subsequent recharge (or cash withdrawal) must operate both assets at the same time according to the current asset ratio

We call this Use Case DODO Vending Machine.

Use Case 3 Completely free market-making algorithm

This use case is for market makers who are ambitious and want to make a big difference. (Market makers can also be project parties or individuals)

For example:

For example:

• Make a market around ETH=700USDT, use a very small k to obtain very competitive liquidity, and earn a lot of handling fees. When it is detected that ETH is expected to rise, the ETH inventory is withdrawn to reduce unilateral risks. But this operation does not weaken buying liquidity.

• The new asset issuance project party only provides tokens but not funds. Token sale starts at 1$. In order to allow more people to buy tokens at a reasonable price, a smaller k is set to make the token rise moderately. Later, when the project party finds that it needs to use funds, it can directly withdraw the assets in the fund pool without damaging the liquidity of the selling order, that is, users can still buy a large number of cheap tokens.

The settings are as follows:

• Only market makers can deposit and withdraw, allowing single-currency operations

We call this Use Case DODO Private Pool.

Use Case 4 Liquidity Crowdfunding

We can divide new asset issuance into two phases:

1. Do not open spot trading, all people participating in the sale will get tokens at the same price

2. Start the spot transaction at the end price of the previous stage, and use the remaining tokens and assets from the previous stage to establish a DODO Vending Machine

We call this Use Case CrowdPooling.

Use Case 5 degenerates to AMM

The PPM algorithm behaves the same as the AMM when the following conditions are satisfied.

• set k=1

• The two assets must be deposited and withdrawn at the same time according to the current price ratio

This also means that AMM is a special case of PMM. The derivation process is as follows:

The price formula of AMM is xy = k, where k is a constant, and x and y represent the quantity of the two tokens respectively. To avoid ambiguity in letters, we define the constant product in the AMM formula as Const and rewrite it as y=Const/x.

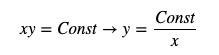
Among them, y represents the stock of quote token, x represents the stock of base token, and the price can be written as the derivative of y (note that the absolute value must be added here, because the price is a positive number).

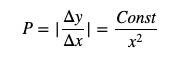
Going back to the PMM formula for k=1, we can write it as:

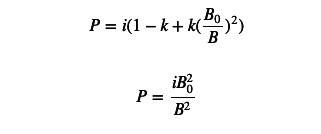
We found that the numerator of the PMM price formula is a constant, and the denominator is the stock of base token. as long as the order

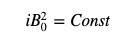
The pricing formula of AMM is consistent with the pricing formula of PMM!

Use Case 6 Stablecoin Trading

The settings are as follows:

• i=1

• k=0.001 (the smaller the value, the closer to the rigid exchange of stablecoins)

The performance of the algorithm can be the same as that of curve, and it is more flexible. It can be closer to rigid exchange than curve, or closer to AMM.

Written by: Radar Bear, Founder of DODO