원래 제목: "Dry goods | How Schnorr signatures can Improve Bitcoin", 저자 Stepan
Blockstream의 MuSig 논문을 읽는 동안 저는 이것이 비트코인 사용자로서 저에게 의미하는 바를 계속 상상했습니다. Schnorr 서명의 일부 기능은 정말 멋지고 편리하며 일부 기능은 매우 성가신 것으로 나타났습니다. 이 글에서 여러분과 제 생각을 나누고 싶습니다. 하지만 먼저 간단히 요약해 보겠습니다.
타원 곡선 서명 알고리즘
현재 비트코인 소유권 시스템은 ECDSA(Elliptic Curve Signature Algorithm)를 사용합니다. 메시지 m에 서명할 때 먼저 메시지를 해시하여 해시 값을 얻습니다. 즉, z = hash(m) 입니다. 우리는 또한 무작위(또는 적어도 무작위로 보이는) 숫자 k가 필요합니다. 여기에서 우리는 난수 생성기를 신뢰하고 싶지 않기 때문에(표준 이하의 난수 생성기와 관련된 버그 및 버그가 너무 많음) 일반적으로 우리가 알고 있는 비밀 값을 기반으로 RFC6979를 사용하고 메시지에 서명하고 계산합니다. 결정적 k.
개인 키 pk를 사용하여 두 개의 숫자로 구성된 메시지 m에 대한 서명을 생성할 수 있습니다. r(임의의 점 R = k * G의 x 좌표) 및 s = (z + r*pk)/k.
이미지 설명
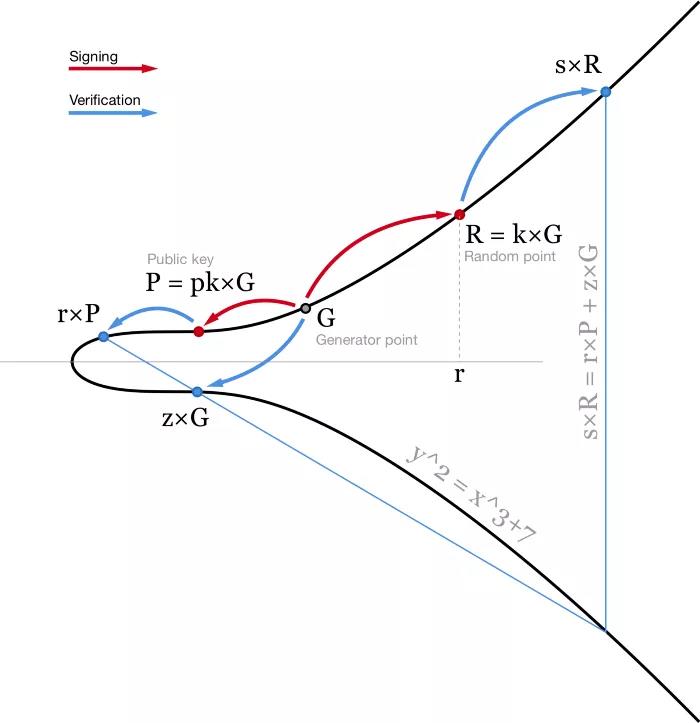
- ECDSA 알고리즘 다이어그램. 설명을 위해 타원 곡선은 실수 영역에서 작동합니다.
이 알고리즘은 매우 일반적이며 사용하기 매우 쉽습니다. 그러나 여전히 개선의 여지가 있습니다. 첫째, 서명 검증은 나눗셈(1/s)과 두 개의 점 곱셈을 포함하며 이러한 작업은 매우 계산 집약적입니다. 비트코인 네트워크에서는 모든 노드가 모든 트랜잭션을 확인해야 하므로 네트워크에서 트랜잭션을 보낼 때 전체 네트워크의 수천 개의 노드가 서명을 확인해야 합니다. 따라서 서명 프로세스가 더 비싸더라도 서명을 더 쉽게 확인할 수 있도록 하는 것이 여전히 매우 유용합니다.
슈노르 서명
슈노르 서명
이미지 설명
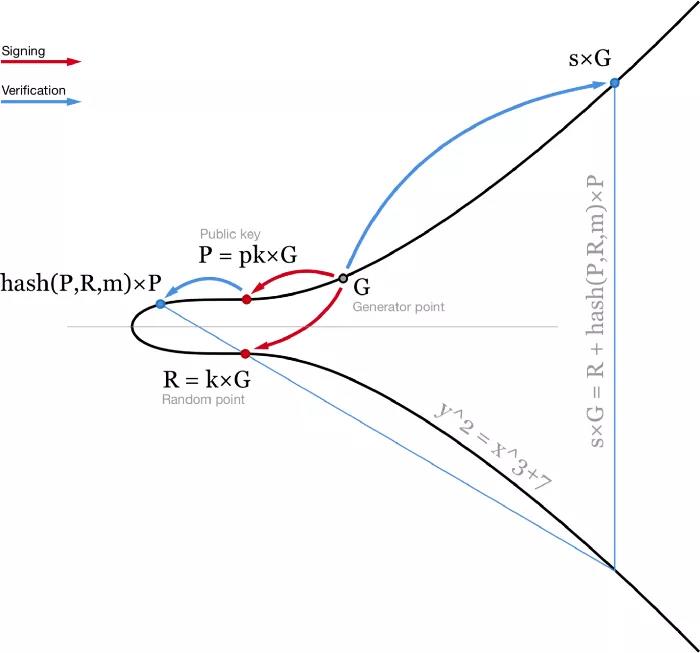
- Schnorr 서명 및 검증 다이어그램 작성 -
이 방정식은 선형이므로 등호가 유지되는 동안 여러 방정식을 더하거나 뺄 수 있습니다. 이것은 Schnorr 서명의 몇 가지 좋은 속성을 제공합니다.
1. 일괄 검증
블록체인에서 블록을 검증할 때 블록에 있는 모든 트랜잭션의 서명이 유효한지 확인해야 합니다. 그 중 하나가 유효하지 않으면 어느 것이든 상관 없습니다. 전체 블록을 거부해야 합니다.
ECDSA의 각 서명은 구체적으로 검증되어야 합니다. 즉, 블록에 1000개의 서명이 포함된 경우 1000개의 나누기와 2000개의 점 곱셈을 계산해야 하므로 총 약 3000개의 무거운 연산이 필요합니다.
그러나 Schnorr 서명을 사용하면 모든 서명 확인 방정식을 합산하고 일부 계산을 절약할 수 있습니다. 1000개의 트랜잭션 블록에서 다음을 확인할 수 있습니다.
(s1+s2+…+s1000) × G=(R1+…+R1000)+(hash(P1,R1,m1)×P1+ hash(P2,R2,m2)×P2+…+hash(P1000,R1000,m1000)×P1000)
이미지 설명
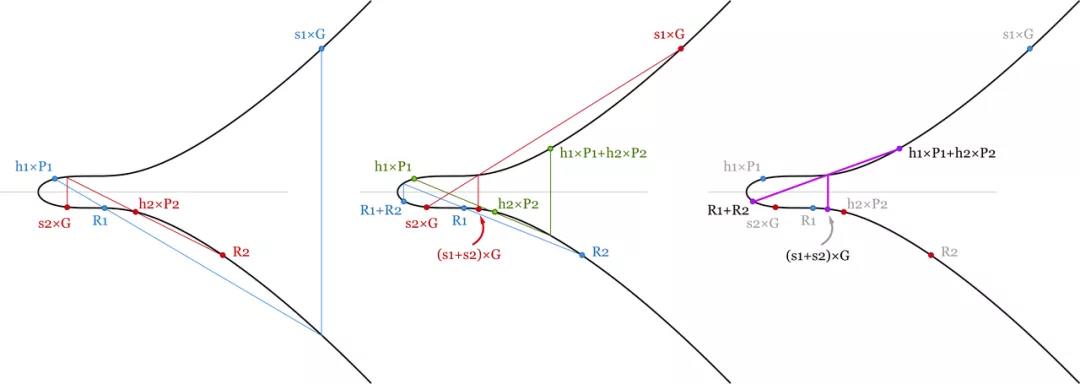
- 두 서명의 일괄 검증. 검증 방정식은 선형적으로 가산되므로 모든 서명이 유효한 한 이러한 방정식의 합계도 설정해야 합니다. 스칼라와 점 덧셈이 점 곱셈보다 훨씬 계산하기 쉽기 때문에 일부 계산을 절약합니다. -
2. 키 생성
우리는 비트코인을 안전하게 유지하고 싶기 때문에 적어도 두 개의 서로 다른 개인 키로 비트코인을 제어하고 싶을 것입니다. 하나는 노트북이나 휴대폰(온라인 지갑, 핫 지갑)에서 사용하고 다른 하나는 하드웨어 지갑/콜드 지갑에 보관합니다. 그중 하나가 유출되더라도 우리는 여전히 비트코인을 통제합니다.
현재 이러한 지갑을 구현하는 방법은 2-2 다중 서명 스크립트를 통하는 것입니다. 즉, 트랜잭션은 두 개의 독립적인 서명을 포함해야 합니다.
Schnorr 서명을 사용하면 한 쌍의 키(pk1,pk2)를 가져오고 공유 공개 키 P = P1 + P2 = pk1 * G + pk2 * G를 사용하여 공통 서명을 생성할 수 있습니다. 서명을 생성할 때 두 장치에서 난수(k1, k2)를 생성하고 두 개의 임의 지점 Ri = ki * G를 생성하고 해시(P, R1 + R2, m )를 추가하면 s1을 얻을 수 있습니다. 및 s2 (si = ki + hash(P, R, m)* pki 이기 때문에). 마지막으로, 공유 공개 키로 확인할 수 있는 공유 서명인 서명 (R, s) = (R1+R2, s1+s2)를 얻기 위해 모두 추가합니다. 집계된 서명인지 다른 사람은 알 수 없으며 일반적인 Schnorr 서명처럼 보입니다.
그러나 이 방법에는 세 가지 문제점이 있습니다.
첫 번째 문제는 UI에 있습니다. 트랜잭션을 시작하려면 공통 R을 계산하고 서명하기 위해 두 장치 간에 여러 라운드의 상호 작용을 시작해야 합니다. 두 개인 키의 경우 콜드 월렛을 한 번만 방문하면 됩니다. 핫 월렛에서 서명할 트랜잭션을 준비하고 k1을 선택하고 R1 = k1 * G를 생성한 다음 서명할 트랜잭션을 함께 넣을 수 있습니다. 이 데이터로 콜드 월렛을 전달하고 서명하십시오. R1이 이미 존재하기 때문에 콜드월렛에서는 한 번의 라운드만으로 서명 거래가 완료될 수 있습니다. 콜드 월렛에서 R2와 s2를 가져와 핫 월렛으로 다시 보냅니다. Hot Wallet은 앞서 언급한 (k1, R1) 서명 트랜잭션을 사용하며, 두 서명의 합은 트랜잭션을 외부 세계로 브로드캐스트할 수 있습니다.
이 경험은 지금 우리가 할 수 있는 것과 다르지 않으며 추가 개인 키를 추가할 때마다 문제가 더 복잡해집니다. 10개의 개인 키로 공동 관리되는 재산이 있고 10개의 개인 키가 세계 각지에 저장되어 있다고 가정하면 지금 거래를 보내는 것이 얼마나 번거로운 일입니까! 현재 ECDSA 알고리즘에서는 각 장치를 한 번만 방문하면 되지만 Schnorr의 키 집계를 사용하는 경우 두 번 방문해야 Ri를 모두 받고 서명할 수 있습니다. 이 경우 집계 대신 각 개인 키로 개별적으로 서명하는 것이 더 나을 수 있으므로 한 라운드의 상호 작용만 필요합니다.
기사가 끝난 후 Manu Drijvers로부터 피드백을 받았습니다. 입증할 수 있는 보안 다중 서명 체계에서는 3라운드의 상호 작용이 필요합니다.
난수 ki와 해당 난수 Ri = ki \G를 선택한 다음 각 장치에 Ri의 해시 값 ti=hash(Ri)를 알려주면 각 장치는 다른 사람의 난수 변경 아이디어를 모른다는 것을 확인할 수 있습니다*
징후
징후
두 번째 문제는 알려진 Rogue 키 공격입니다. 논문에 아주 잘 설명되어 있으므로 자세한 내용은 다루지 않겠습니다. 이는 아마도 귀하의 장치 중 하나가 해킹(예: 핫 월렛 하이재킹)되고 공개 키가 (P1 - P2)인 것처럼 가장하는 경우 개인 키로만 두 개인 키의 공유 개인 키를 제어할 수 있음을 의미합니다. 키 pk1 자금. 간단한 해결책은 장치를 설정할 때 해당 공개 키에 서명하기 위해 개인 키를 요구하는 것입니다.
세 번째 주요 문제가 있습니다. 결정적 k로 서명할 수 없습니다. 결정적 k를 사용하면 해커가 단 한 번의 간단한 공격으로 개인 키를 얻을 수 있습니다. 공격 방법은 다음과 같습니다. 일부 해커가 노트북을 해킹하여 개인 키(예: pk1) 중 하나를 완전히 제어합니다. 비트코인을 사용하려면 pk1과 pk2의 통합 서명이 필요하기 때문에 자금이 여전히 안전하다고 생각합니다. 그래서 평소처럼 트랜잭션을 시작하고 서명할 트랜잭션을 준비하고 R1을 하드웨어 지갑으로 보내고 하드웨어 지갑이 서명한 후 (R2, s2)를 다시 핫 지갑으로 보냅니다... 그런 다음 핫 지갑에 오류가 발생하여 서명 및 방송을 완료할 수 없습니다. 그래서 우리는 다시 시도하지만 이번에는 해킹된 컴퓨터가 다른 난수인 R1'을 사용합니다. 하드웨어 지갑에서 동일한 트랜잭션에 서명하고 (R2, s2')를 해킹된 컴퓨터로 다시 보냈습니다. 이번에는 더 이상 없습니다. 모든 비트코인이 사라졌습니다.
이 공격에서 해커는 동일한 트랜잭션의 두 가지 유효한 서명((R1, s1, R2, s2) 및 (R1', s1', R2, s2'))을 획득했습니다. 이 R2는 같지만 R = R1 + R2와 R' = R1' + R2는 다릅니다. 이는 해커가 두 번째 개인 키를 계산할 수 있음을 의미합니다. s2-s2'=(hash(P,R1+R2,m)-hash(P,R1'+R2,m))⋅pk2 또는 pk2 =(s2-s2 ')/(해시(P,R1+R2,m)-해시(P,R1'+R2,m)). 이것이 키 집계에서 가장 불편한 부분이라고 생각합니다. 안전한 집계를 위해 매번 좋은 난수 생성기를 사용해야 합니다.
3. Musig
MuSig는 문제 중 하나를 해결했습니다. 악성 키 공격은 더 이상 작동하지 않습니다. 여기서 목표는 공개 키에 해당하는 개인 키가 있음을 증명할 필요 없이 여러 당사자/여러 설정의 서명과 공개 키를 집계하는 것입니다.
집계된 서명은 집계된 공개 키에 해당합니다. 그러나 MuSig에서는 모든 공동 서명자의 공개 키를 직접 추가하는 대신 일부 매개변수를 곱하여 집계된 공개 키 P = hash(L,P1)×P1 + ... + hash(L,Pn ) ×Pn. 여기서 L = hash(P1,...,Pn) - 이 공개 번호는 모든 공개 키를 기반으로 합니다. L의 비선형 속성은 공격자가 공격을 시작하기 위해 특수 공개 키를 구성하는 것을 방지합니다. 공격자가 자신의 해시(L,Patk)×Patk가 무엇인지 알고 있더라도 그것으로부터 Patk를 추론할 수 없습니다. 이는 공개 키에서 개인 키를 추론하려는 것과 같습니다.
서명 구성의 다른 프로세스는 위에서 설명한 것과 매우 유사합니다. 서명을 생성할 때 각 공동 서명자는 난수 ki를 선택하고 Ri = ki * G를 다른 사람과 공유합니다. 그런 다음 모든 임의의 점을 더하여 R=R1+…+Rn 을 얻은 다음 서명 si = ki + hash(P,R,m) ⋅ hash(L,Pi) ⋅ pki 를 생성합니다. 따라서 집계된 서명은 (R, s)=(R1+…+Rn, s1+…+sn) 이며 서명을 확인하는 방법은 이전과 동일합니다. s×G = R + hash(P,R,m )×피.
4. 머클 트리 다중 서명
또한 MuSig 및 키 집계에는 *모든 서명자가 트랜잭션에 서명*해야 한다는 사실을 눈치채셨을 것입니다. 하지만 원하는 것이 2-3 다중 서명 스크립트라면 어떨까요? 이 시점에서 서명 집계를 사용할 수 있습니까, 아니면 일반적인 OP_CHECKMULTISIG를 사용하고 별도로 서명해야 합니까? (번역자 주: OP_CHECKMULTISIG는 비트코인이 타원 곡선 다중 서명 스크립트를 검증하기 위한 연산 코드입니다.)
예, 대답부터 시작하겠습니다. 하지만 합의는 약간 다를 것입니다. 집계 서명이 공개 키 Merkle 트리의 요소에 해당하는지 여부를 확인한다는 점을 제외하면 OP_CHECKMULTISIG와 유사한 opcode를 개발할 수 있습니다.
예를 들어 공개 키 P1, P2 및 P3을 사용하여 2-3 다중 서명 스크립트를 구성하려면 이러한 공개 키 쌍(P1, P2), (P2, P3), (P1 , P3) Merkle 트리를 빌드하고 잠금 스크립트에 Merkle 트리의 루트를 게시합니다.
텍스트
그러나 Merkle 공개 키 트리를 사용하면 백만 개의 다중 서명 스크립트로 제한할 필요가 없습니다. 공개 키 조합을 사용하여 트리를 만들 수 있습니다. 예를 들어 노트북, 휴대폰, 하드웨어 지갑, 니모닉이 있다면 노트북+하드웨어 지갑, 휴대폰+하드웨어 지갑을 사용하거나 별도의 암기단어를 사용하여 비트코인을 사용할 수 있는 머클트리를 구축할 수 있습니다. . 이것은 현재 OP_CHECKMULTISIG가 할 수 없는 것입니다. "IF - Else" 스타일 흐름 제어를 사용하여 더 복잡한 스크립트를 구성하지 않는 한 말입니다.
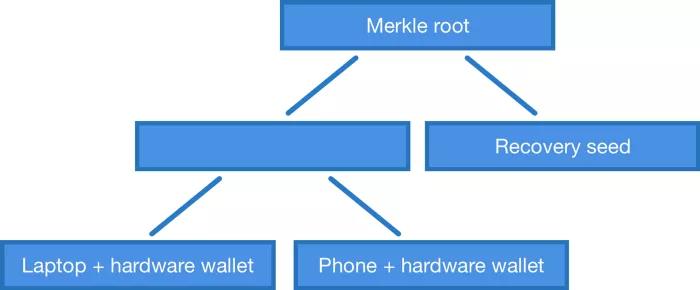
결론적으로
Schnorr 서명은 훌륭하며 블록 검증에서 일부 계산 오버헤드를 해결하고 키 집계도 제공합니다. 후자는 사용하기 다소 불편하지만 우리는 사람들이 그것을 사용하도록 강요하지 않습니다. 어쨌든 개별적이고 집계되지 않은 서명을 사용하여 일반적인 다중 서명 체계를 사용할 수 있습니다.
저는 Schnorr 서명을 사용하기를 기다릴 수 없습니다. 바라건대 Bitcoin 프로토콜이 곧 이를 통합할 것입니다.
(위에)
(위에)





