효율적인 시장에는 가격에 대한 시장의 판단을 전달하는 엄청난 양의 정보가 포함되어 있습니다. 그러나 체인의 컴퓨팅 리소스는 제한적이므로 체인에서 매우 유연한 시장을 실현하는 것은 코끼리를 냉장고에 넣는 것과 같습니다.

냉장고에 코끼리를 채우는 것은 드문 일이 아니며 인터넷 역사상 몇 가지 위업이 있었습니다. 이미지 압축, 오디오 압축 등.

압축의 본질은 가장 중요한 기능을 추출하고 중요하지 않은 세부 정보를 버리는 것입니다.

그래서 시장의 가장 중요한 특징은 유동성입니다. 유동성은 깊이 맵으로 나타낼 수 있습니다.

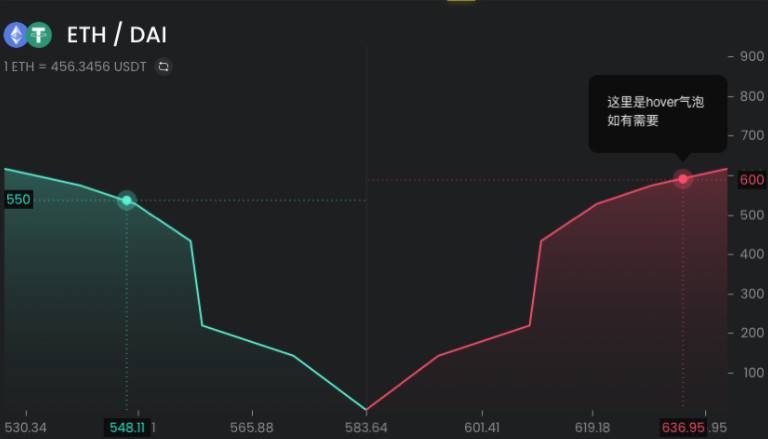
아래 그림에서 깊이 맵을 두 개의 삼각형으로 추상화할 수 있으며 이 두 삼각형을 설명하려면 중간 가격과 기울기만 있으면 됩니다.

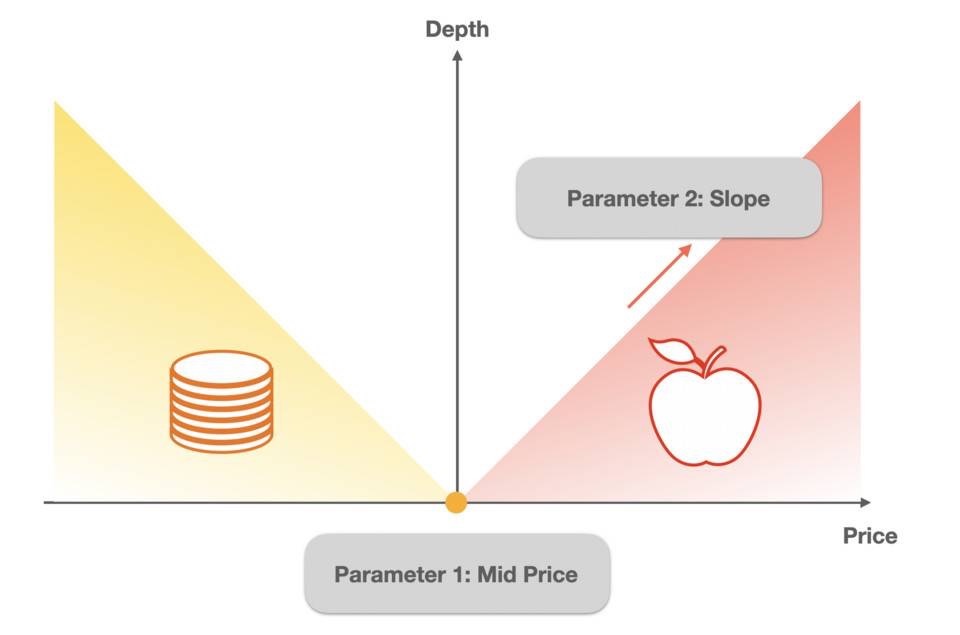
우측의 매도 사다리꼴의 깊이에 초점을 맞추는데, 가장 큰 특징은 Base Token을 많이 매수할수록 가격이 높아진다는 것입니다. 따라서 이 선형 깊이는 다음과 같이 표현할 수 있습니다.

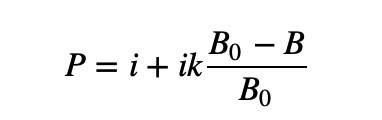
여기서 i는 첫 번째 매개변수 "중간 가격"이고 k는 두 번째 매개변수 "기울기"입니다.

B는 현재 기본 토큰 재고를 나타내고 B0은 초기 기본 토큰 재고를 나타내며 (B0-B)/B0은 소비된 BaseToken의 백분율을 나타내는 데 사용됩니다.

이 공식은 판매된 기본 토큰의 수에 따라 가격을 선형적으로 증가시킬 수 있습니다.

하지만 정말 선형이 이동성을 설명하는 가장 좋은 방법일까요? 아니요, 선형 설명에는 두 가지 제한이 있습니다.

1. 실물시장에서는 대부분의 유동성이 시장의 중간가격 근처에 집중되어 있으며, 선형적인 설명은 이러한 불균형한 분포를 반영하지 않습니다.

2. 가격이 시장의 중간 가격에서 크게 벗어나더라도 유동성이 있어야 하며 선형 설명 아래의 가격에는 상한과 하한이 있습니다.

우리는 가격 곡선에 비선형성을 도입합니다. 매개 변수를 확장하지 않는다는 전제하에 깊이 분포는 시장 규칙에 더 부합하고 유연성이 더 높습니다.

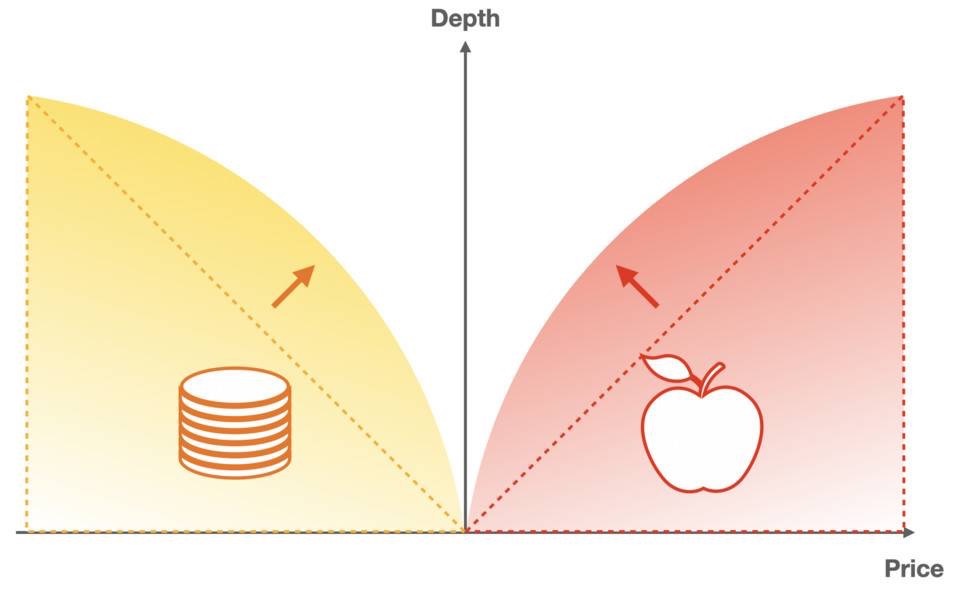
가장 간단한 비선형 솔루션은 덧셈 대신 곱셈을 사용하는 것입니다.

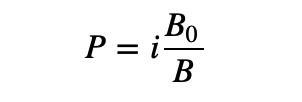
이 공식은 B가 감소함에 따라 P가 무한대까지 계속 증가한다는 것을 만족시킬 수 있습니다. 그러나 기울기의 효과를 어떻게 추가합니까?

이렇게 하려면 B0/B 항목을 수정해야 합니다. B0/B≥1, 매개변수를 사용하여 크기를 조정하고 이 값을 1보다 크거나 같게 유지하면서 "1보다 큰 정도"를 제어할 수 있습니다.

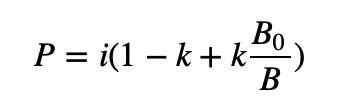
위 공식에서 k의 값 범위는 [0,1]이며 가격의 기울기를 결정합니다.

• k=0일 때 가격은 완전히 변하지 않습니다.

• k=1일 때 가격 기울기는 공식의 이전 버전으로 퇴보합니다.

• k가 클수록 가격 변동에 더 민감합니다. k가 작을수록 가격 변동에 덜 민감합니다.

그러나 여전히 작은 문제가 있습니다. 여기서 P는 한계 가격이고 한계 가격에 대한 적분은 사용자가 지불해야 하는 자산의 양입니다. 위 공식에서 B0/B의 적분 뒤에 로그 함수가 나타나므로 후속 계산이 매우 복잡해집니다. 이 문제를 방지하기 위해 한 단계 더 진행합니다.

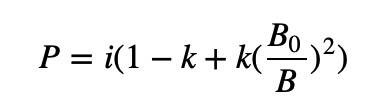
B0/B 외부에 제곱항을 추가하여 적분 후 단순한 나눗셈이 되도록 합니다.

놀랍게도 k=1일 때 이 곡선은 정확히 AMM에서 정의한 접합 곡선입니다. 이 우연은 이것이 시장의 본질에 더 많이 닿는 일련의 알고리즘이라고 믿게 만듭니다.

마찬가지로 왼쪽 절반의 깊이 맵의 경우 대칭적 접근 방식을 사용하여 기본 토큰을 인용 토큰으로 바꾸고 곱셈을 나누기로 바꿉니다.

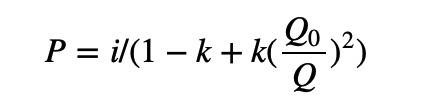
왼쪽과 오른쪽의 깊이 맵을 결합하여 PMM 알고리즘의 전체 버전을 얻고 정렬합니다.

PMM 알고리즘은 매개변수가 단순하지만 매우 유연한 고도로 압축된 주문서 시장입니다.

이것은 우리가 냉장고의 작은 공간에서 코끼리의 힘을 가질 수 있게 합니다.

이 알고리즘이 매개변수와 입출금 규칙을 조정하여 달성할 수 있는 사용 사례를 나열하겠습니다.

Use Case 1 외부 시장 가격에 따른 적극적인 시장 조성

이 사용 사례의 응용 시나리오는 ETH, BTC 등과 같은 거대한 외부 시장이 있는 주류 통화입니다.

PMM은 핸디캡 가격의 적극적인 조정을 실현하고 IL을 줄일 수 있습니다. AMM보다 높은 자본 활용률을 확보하고 유동성을 제공하기 위해 단일 통화를 보유합니다.

설정은 다음과 같습니다.

• 가격 i를 외부 시장 가격으로 설정

• k를 1보다 작은 숫자로 설정

• 누구나 일방적으로 입출금 가능

이 사용 사례를 DODO Classic 풀이라고 합니다.

사용 사례 2 가벼운 자본 요구 사항을 위한 자동 시장 조성 알고리즘

이 사용 사례는 주관적인 가격 결정력이 없는 롱테일 통화 시장에 적용되며 가격 결정력은 테이커에게 완전히 이양됩니다.

일반적으로 롱테일 코인은 새로운 자산이며 AMM 프레임워크에서 판매 유동성이 충분하지 않아 장기적으로 유동성이 부족합니다.

설정은 다음과 같습니다.

• 가격 i를 초기 발행 가격으로 설정

• k를 임의로 설정

• 첫 번째 충전은 시장 가격을 변경하지 않고 자산 비율에 관계없이 가능합니다.

• 후속 충전(또는 현금 인출)은 현재 자산 비율에 따라 두 자산을 동시에 운영해야 합니다.

우리는 이것을 DODO 자판기라고 부릅니다.

사용 사례 3 완전 무료 시장 조성 알고리즘

이 사용 사례는 야심차고 큰 차이를 만들고자 하는 마켓 메이커를 위한 것입니다. (마켓 메이커는 프로젝트 당사자 또는 개인일 수도 있음)

예를 들어:

예를 들어:

• ETH=700USDT 정도의 시장을 만들고, 아주 작은 k를 사용하여 매우 경쟁력 있는 유동성을 얻고, 많은 취급 수수료를 얻습니다. ETH가 상승할 것으로 예상되는 경우 일방적인 위험을 줄이기 위해 ETH 재고를 회수합니다. 그러나이 작업은 구매 유동성을 약화시키지 않습니다.

• 새로운 자산 발행 프로젝트 당사자는 토큰만 제공하고 자금은 제공하지 않습니다. 토큰 판매는 1$부터 시작됩니다. 더 많은 사람들이 합리적인 가격으로 토큰을 살 수 있도록 하기 위해 k를 작게 설정하여 토큰이 적당히 상승하도록 합니다. 나중에 프로젝트 당사자가 자금을 사용해야 한다는 것을 알게 되면 판매 주문의 유동성을 손상시키지 않고 자금 풀의 자산을 직접 인출할 수 있습니다. 즉, 사용자는 여전히 많은 수의 저렴한 토큰을 구입할 수 있습니다.

설정은 다음과 같습니다.

• 마켓메이커만 입금 및 출금이 가능하여 단일 통화 운영이 가능합니다.

이 사용 사례를 DODO Private Pool이라고 합니다.

사용 사례 4 유동성 크라우드 펀딩

새로운 자산 발행은 두 단계로 나눌 수 있습니다.

1. 현물 거래를 열지 마십시오. 판매에 참여하는 모든 사람들은 동일한 가격으로 토큰을 받게 됩니다.

2. 이전 단계의 종가에서 현물 거래를 시작하고, 이전 단계의 남은 토큰과 자산을 사용하여 DODO 자판기 구축

이 사용 사례를 CrowdPooling이라고 합니다.

사용 사례 5는 AMM으로 퇴보

PPM 알고리즘은 다음 조건을 만족할 때 AMM과 동일하게 동작합니다.

• k=1로 설정

• 두 자산은 현재 가격 비율에 따라 동시에 입금 및 출금되어야 합니다.

이것은 또한 AMM이 PMM의 특별한 경우임을 의미합니다. 도출 과정은 다음과 같습니다.

AMM의 가격 공식은 xy = k입니다. 여기서 k는 상수이고 x와 y는 각각 두 토큰의 수량을 나타냅니다. 문자의 모호성을 피하기 위해 AMM 공식의 상수 곱을 Const로 정의하고 y=Const/x로 다시 작성합니다.

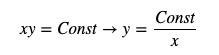
그 중 y는 호가토큰의 재고량, x는 기준토큰의 재고량을 나타내며 가격은 y의 미분으로 쓸 수 있다(여기서 가격은 양수이므로 절대값을 더해야 함).

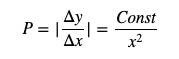
k=1에 대한 PMM 공식으로 돌아가서 다음과 같이 작성할 수 있습니다.

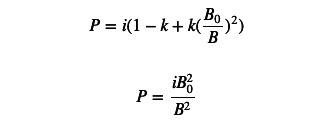
우리는 PMM 가격 공식의 분자가 상수이고 분모가 기본 토큰의 재고임을 발견했습니다. 주문만큼

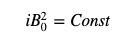
AMM의 가격 공식은 PMM의 가격 공식과 일치합니다!

사용 사례 6 스테이블 코인 거래

설정은 다음과 같습니다.

• i=1

• k=0.001 (값이 작을수록 안정적인 스테이블코인 교환에 가깝습니다.)

알고리즘의 성능은 곡선과 같을 수 있고 더 유연할 수 있으며 곡선보다 강체 교환에 가까울 수도 있고 AMM에 가까울 수도 있습니다.

작성자: Radar Bear, DODO 설립자