原題:「Dry Goods | How Schnorr Signature can Improvement Bitcoin」、著者 Stepan

Blockstream による MuSig 論文を読みながら、これがビットコイン ユーザーである私にとって何を意味するのかを想像し続けました。 Schnorr 署名のいくつかの機能は非常にクールで便利ですが、いくつかの機能は非常に面倒であることがわかりました。この記事では、私の考えを皆さんと共有できればと思っています。まず最初に、簡単にまとめてみましょう。

楕円曲線署名アルゴリズム

現在のビットコイン所有権システムは ECDSA (楕円曲線署名アルゴリズム) を使用しています。メッセージ m に署名するときは、まずメッセージをハッシュしてハッシュ値を取得します (つまり、 z = hash(m) )。ランダムな (少なくとも一見ランダムな) 数値 k も必要です。ここでは、乱数生成器を信頼したくないので (標準以下の乱数生成器に関連するバグやバグが多すぎます)、通常は RFC6979 を使用します。既知の秘密の値に基づいて、メッセージに署名したり、計算したりする必要があります。決定論的なk。

秘密鍵 pk を使用すると、r (ランダム点の x 座標 R = k * G) と s = (z + r*pk)/k の 2 つの数値で構成されるメッセージ m の署名を生成できます。

画像の説明

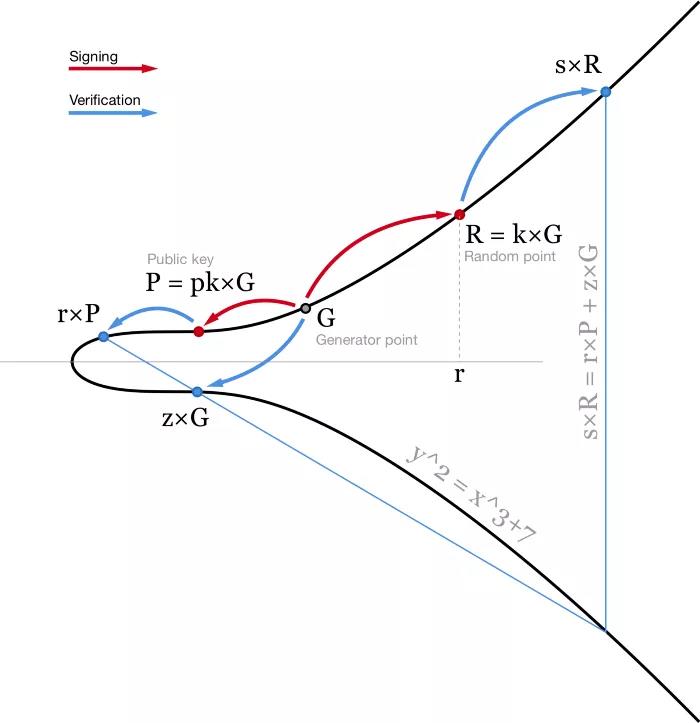
- ECDSA アルゴリズム図。説明のために、楕円曲線は実数のフィールド上で動作します-

このアルゴリズムは非常に一般的であり、非常に使いやすいです。しかし、まだ改善の余地があります。まず、署名の検証には除算 (1/s) と 2 つのドット乗算が含まれており、これらの演算は非常に大量の計算を要します。ビットコイン ネットワークでは、すべてのノードがすべてのトランザクションを検証する必要があるため、ネットワークにトランザクションを送信すると、ネットワーク全体の何千ものノードが署名を検証する必要があります。したがって、たとえ署名プロセスのコストが高くなったとしても、署名の検証を容易にすることは依然として非常に有益です。

シュノアの署名

シュノアの署名

画像の説明

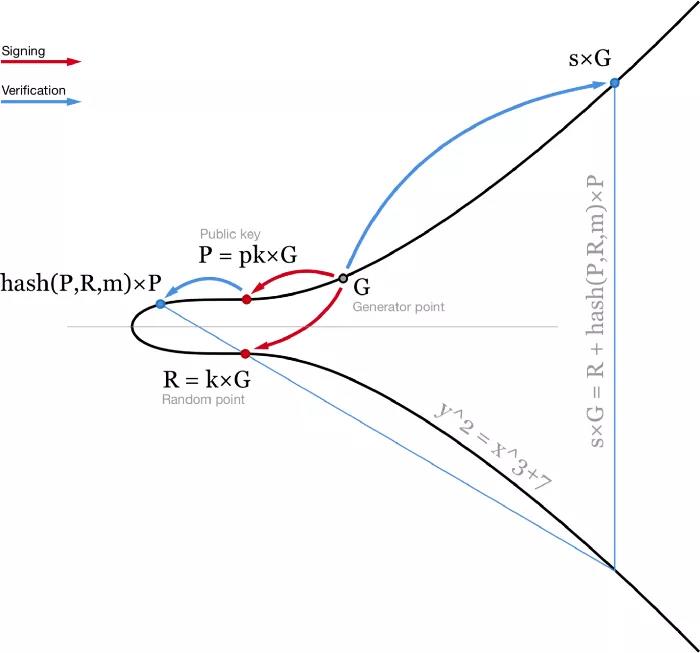
- Schnorr の署名と検証の図解 -

この方程式は線形であるため、等号が維持されたまま複数の方程式を加算および減算することができます。これにより、Schnorr 署名のいくつかの優れた特性が得られます。

1. 一括検証

ブロックチェーン上のブロックを検証するときは、ブロック内のすべてのトランザクションの署名が有効であることを検証する必要があります。それらの 1 つが無効な場合、どれが無効であるかは問題ではありません。ブロック全体を拒否する必要があります。

ECDSA の各署名は具体的に検証する必要があります。つまり、ブロックに 1000 個の署名が含まれている場合、1000 回の除算と 2000 回のポイント乗算を計算する必要があり、合計で約 3000 回の重い演算が必要になります。

しかし、Schnorr 署名を使用すると、すべての署名検証方程式を合計して、計算の一部を節約できます。 1000 件のトランザクションのブロックで、次のことを確認できます。

(s1+s2+…+s1000) × G=(R1+…+R1000)+(hash(P1,R1,m1)×P1+ hash(P2,R2,m2)×P2+…+hash(P1000,R1000,m1000)×P1000)

画像の説明

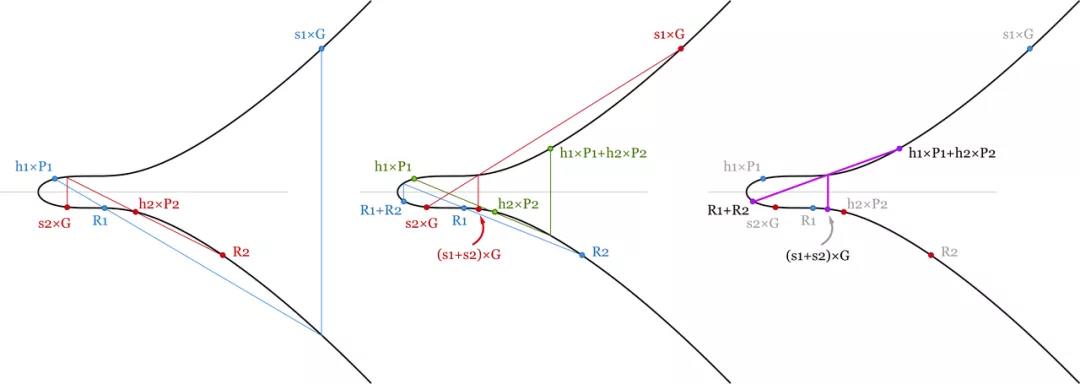
- 2 つの署名の一括検証。検証式は線形加算であるため、すべての署名が有効である限り、これらの式の合計も確立する必要があります。スカラーと点の加算は点の乗算よりもはるかに簡単に計算できるため、一部の計算を節約できます。 -

2. 鍵の生成

私たちはビットコインを安全に保ちたいので、おそらく少なくとも 2 つの異なる秘密鍵を使用してビットコインを管理したいと考えています。 1 つはラップトップまたは携帯電話 (オンライン ウォレット、ホット ウォレット) で使用され、もう 1 つはハードウェア ウォレット/コールド ウォレットに保管されます。たとえそのうちの1つが漏洩したとしても、私たちは依然としてビットコインを管理しています。

現在、このようなウォレットを実装する方法は、2-2 マルチ署名スクリプトを使用することです。つまり、トランザクションには 2 つの独立した署名が含まれている必要があります。

Schnorr 署名を使用すると、鍵のペア (pk1、pk2) を取得し、共有公開鍵 P = P1 + P2 = pk1 * G + pk2 * G を使用して共通の署名を生成できます。署名を生成するときは、2 つのデバイスで乱数 (k1, k2) を生成し、2 つのランダム点 Ri = ki * G を生成し、ハッシュ(P, R1 + R2, m ) を追加する必要があります。s1 を取得できます。および s2 (si = ki + hash(P, R, m)* pki であるため)。最後に、それらをすべて加算して署名 (R, s) = (R1+R2, s1+s2) を取得します。これは共有署名であり、共有公開キーで検証できます。それが集約された署名であるかどうかは他の誰にもわかりません。見た目は通常の Schnorr 署名とまったく同じです。

ただし、このアプローチには 3 つの問題があります。

最初の問題は UI にあります。トランザクションを開始するには、共通の R の計算と署名のため、2 つのデバイス上で複数ラウンドの対話を開始する必要があります。 2 つの秘密鍵の場合、コールド ウォレットにアクセスする必要があるのは 1 回だけです。ホット ウォレットで署名するトランザクションを準備し、k1 を選択して R1 = k1 * G を生成し、署名するトランザクションをまとめます。これらのデータをコールドウォレットに渡し、署名します。すでに R1 が存在するため、署名トランザクションはコールド ウォレット内で 1 ラウンドのみで完了できます。コールドウォレットから R2 と s2 を取得し、ホットウォレットに送り返します。ホットウォレットは前述の (k1, R1) 署名トランザクションを使用し、2 つの署名の合計によりトランザクションを外部にブロードキャストできます。

この経験は現在実行できることと何ら変わりません。秘密キーを追加するたびに、問題はさらに複雑になります。 10 個の秘密鍵で共同管理されている資産があり、その 10 個の秘密鍵が世界のさまざまな場所に保管されているとします。この時点でトランザクションを送信するのは、どれほど面倒なことでしょう。現在の ECDSA アルゴリズムでは、各デバイスに 1 回アクセスするだけで済みますが、Schnorr のキー集約を使用する場合は、すべての Ri を取得して署名するために 2 回アクセスする必要があります。この場合、集約する代わりに、各秘密鍵を個別に使用して署名する方がよい場合があります。これにより、対話が 1 回だけ必要になります。

記事の完成後、Manu Drijvers からフィードバックを受け取りました。安全であると証明されたマルチ署名スキームでは、3 ラウンドの対話が必要です。

• 乱数 ki と対応する乱数点 Ri = ki \G を選択し、各デバイスに Ri のハッシュ値 ti=hash(Ri) を通知すると、各デバイスは他人の乱数変更アイデアを知られないようにすることができます*

• サイン

• サイン

2 番目の問題は、既知の Rogue key 攻撃です。この論文はそれについて非常に詳しく説明しているので、詳細には触れません。これはおそらく、デバイスの 1 つがハッキングされ (たとえば、ホット ウォレットがハイジャックされた)、公開鍵が (P1 - P2) であるふりをした場合、2 つの秘密鍵の共有秘密鍵を秘密鍵でのみ制御できることを意味します。主要なPK1資金。簡単な解決策は、デバイスのセットアップ時に、対応する公開キーに署名するために秘密キーを要求することです。

3番目の大きな問題があります。決定論的な k で署名することはできません。決定論的な k を使用すると、ハッカーは 1 回の簡単な攻撃で秘密鍵を入手できます。攻撃は次のとおりです。一部のハッカーがあなたのラップトップをハッキングし、秘密鍵の 1 つ (pk1 など) を完全に制御します。私たちのビットコインを使用するには pk1 と pk2 の集約された署名が必要であるため、資金はまだ安全であると感じています。そこで、通常どおりトランザクションを開始し、署名されるトランザクションと R1 を準備してハードウェア ウォレットに送信し、ハードウェア ウォレットが署名した後、(R2, s2) をホット ウォレットに送り返します。ウォレットでエラーが発生しました。署名とブロードキャストを完了できません。そこで再試行しますが、今度はハッキングされたコンピュータが別の乱数 R1' を使用します。私たちはハードウェア ウォレットで同じトランザクションに署名し、(R2, s2') をハッキングされたコンピューターに送り返しました。今回はもうありません。私たちのビットコインはすべてなくなりました。

この攻撃では、ハッカーは同じトランザクションの 2 つの有効な署名 (R1, s1, R2, s2) と (R1', s1', R2, s2') を取得しました。このR2は同じですが、R=R1+R2とR'=R1'+R2は異なります。これは、ハッカーが 2 番目の秘密鍵を計算できることを意味します: s2-s2'=(hash(P,R1+R2,m)-hash(P,R1'+R2,m))⋅pk2 または pk2 =(s2-s2 ')/(ハッシュ(P,R1+R2,m)-ハッシュ(P,R1'+R2,m))。これがキー集約の最も不便な部分だと思います。安全に集約するには、毎回優れた乱数ジェネレーターを使用する必要があります。

3. Musig

MuSig は、不正キー攻撃が機能しなくなるという問題の 1 つを解決しました。ここでの目標は、それらの公開鍵に対応する秘密鍵を持っていることを証明する必要なしに、複数の当事者/複数の設定からの署名と公開鍵を集約することです。

集約された署名は、集約された公開鍵に対応します。しかし、MuSig では、すべての共同署名者の公開鍵を直接追加する代わりに、それらにいくつかのパラメータを掛けます。その結果、集合公開鍵 P = hash(L,P1)×P1 + ... + hash(L,Pn) ) ×Pn.ここで、L = hash(P1,...,Pn) - この公開番号はすべての公開キーに基づいています。 L の非線形特性により、攻撃者が特別な公開鍵を構築して攻撃を開始することができなくなります。たとえ攻撃者がハッシュ(L,Patk)×Patk が何であるべきかを知っていたとしても、そこから Patk を推測することはできません。これは、公開鍵から秘密鍵を推測したいのと同じです。

署名構築の他のプロセスは、上で説明したプロセスと非常に似ています。署名を生成するとき、各共同署名者は乱数 ki を選択し、Ri = ki * G を他の署名者と共有します。次に、すべてのランダムな点を合計して R=R1+…+Rn を取得し、署名 si = ki + hash(P,R,m) ⋅ hash(L,Pi) ⋅ pki を生成します。したがって、集約された署名は (R, s)=(R1+…+Rn, s1+…+sn) となり、署名を検証する方法は以前と同じです: s×G = R + hash(P,R,m )×P .

4.マークルツリーマルチシグネチャ

MuSig とキー集約では *すべての署名者がトランザクションに署名する必要があることにも気づいたかもしれません。しかし、やりたいことが 2 ～ 3 個のマルチシグネチャ スクリプトだったらどうなるでしょうか?この時点で署名集約を使用できますか、それとも通常の OP_CHECKMULTISIG を使用して個別に署名する必要がありますか? (翻訳者注: OP_CHECKMULTISIG は、ビットコインが楕円曲線マルチシグネチャ スクリプトを検証するためのオペレーション コードです)

答えから始めましょう、はい、しかし合意は少し異なります。 OP_CHECKMULTISIG と同様のオペコードを開発できますが、集約署名が公開鍵マークル ツリー上の要素に対応するかどうかをチェックする点が異なります。

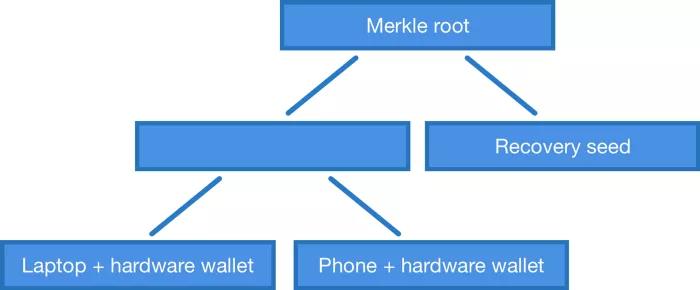
たとえば、公開キー P1、P2、および P3 を使用して 2 ～ 3 の多重署名スクリプトを作成したい場合、これらの公開キーのすべてのペア (P1、P2)、(P2、P3)、(P1) を使用する必要があります。 、P3) マークル ツリーを構築し、ロック スクリプトでマークル ツリーのルートを公開します。

文章

しかし、マークル公開キー ツリーを使用すると、mn 個のマルチ署名スクリプトに制限される必要はありません。公開鍵を任意に組み合わせてツリーを作成できます。たとえば、ラップトップ、電話、ハードウェア ウォレット、ニーモニックがある場合、ラップトップ + ハードウェア ウォレット、電話 + ハードウェア ウォレット、またはビットコインを使用するための別の暗記単語を使用できるマークル ツリーを構築できます。 。これは、「IF - Else」スタイルのフロー制御を使用してより複雑なスクリプトを構築しない限り、現在の OP_CHECKMULTISIG では実行できないことです。

結論は

Schnorr 署名は優れており、ブロック検証における計算オーバーヘッドの一部を解決し、キーの集約も可能にします。後者は使用するのがやや不便ですが、私たちは人々にそれを使用することを強制していません。とにかく、個別の非集約署名を使用して、通常のマルチ署名スキームを使用することができます。

Schnorr 署名を使用するのが待ちきれません。ビットコイン プロトコルにすぐに組み込まれることを願っています。

（以上）

（以上）