Original title: "Dry goods | How Schnorr signatures can improve Bitcoin", author Stepan

While reading the MuSig paper by Blockstream, I kept imagining what this meant for me as a Bitcoin user. I've found some features of Schnorr signatures to be really cool and convenient, and some features to be quite annoying. In this article, I hope to share my thoughts with you. But first, let's do a quick recap.

Elliptic Curve Signature Algorithm

The current Bitcoin ownership system uses ECDSA (Elliptic Curve Signature Algorithm). When signing a message m, we first hash the message to get a hash value, ie z = hash(m) . We also need a random (or at least seemingly random) number k. Here, we don't want to trust the random number generator (there are too many bugs and bugs related to substandard random number generators), so we generally use RFC6979, based on a secret value we know and we want to sign message, calculate a deterministic k.

Using the private key pk , we can generate a signature for message m consisting of two numbers: r (the x-coordinate of a random point R = k * G) and s = (z + r*pk)/k.

image description

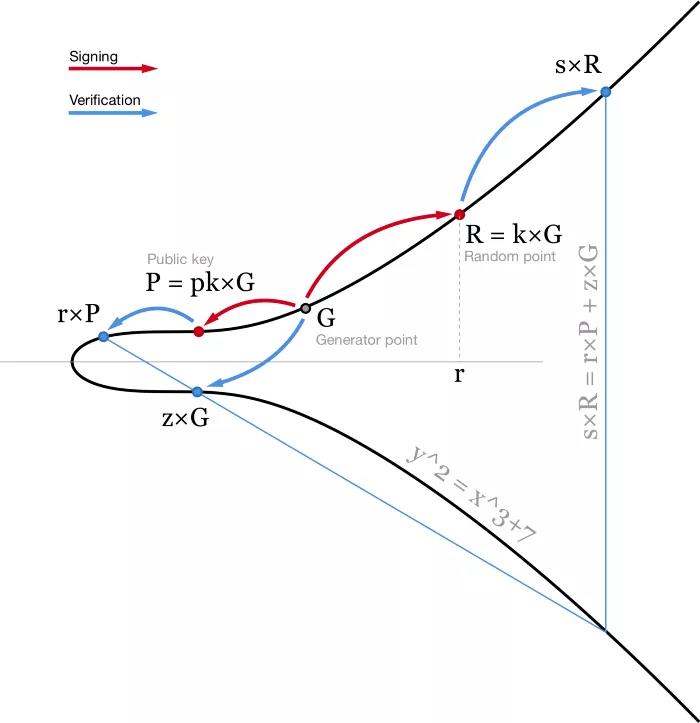
- ECDSA Algorithm Diagram. For illustration purposes, elliptic curves operate over the field of real numbers −

This algorithm is very common and very easy to use. But there is still room for improvement. First, the verification of the signature involves division (1/s) and two dot multiplications, and these operations are very computationally intensive. In the Bitcoin network, every node has to verify every transaction, so when you send a transaction in the network, thousands of nodes in the whole network have to verify your signature. So even if the signing process becomes more expensive, it is still very beneficial to make it easier to verify the signature.

Schnorr signature

Schnorr signature

image description

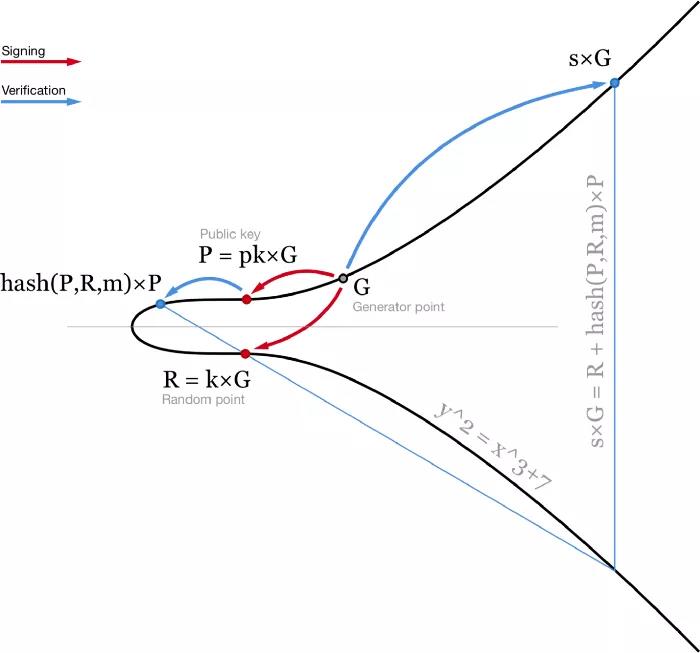
- Diagramming Schnorr Signature and Verification -

This equation is linear, so multiple equations can be added and subtracted while the equality sign still holds. This brings us to several nice properties of Schnorr signatures.

1. Batch verification

When validating a block on the blockchain, we need to verify that the signatures of all transactions in the block are valid. If one of them is invalid, it doesn't matter which one - we have to reject the whole block.

Each signature of ECDSA has to be verified specifically, meaning that if a block contains 1000 signatures, then we need to calculate 1000 divisions and 2000 point multiplications, totaling about 3000 heavy operations.

But with Schnorr signatures, we can add up all the signature verification equations and save some computation. In a block of 1000 transactions, we can verify:

(s1+s2+…+s1000) × G=(R1+…+R1000)+(hash(P1,R1,m1)×P1+ hash(P2,R2,m2)×P2+…+hash(P1000,R1000,m1000)×P1000)

image description

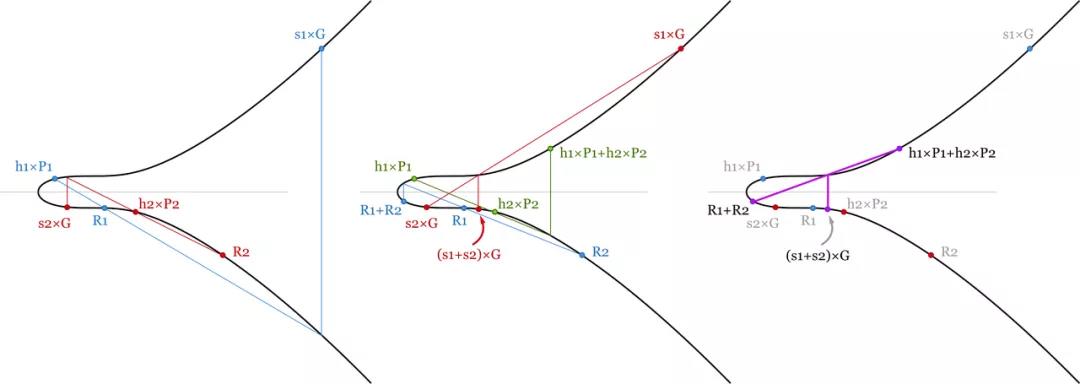
- Batch verification of two signatures. Because the verification equation is linearly additive, as long as all the signatures are valid, the sum of these equations must also be established. We save some computation because scalar and point addition is much easier to compute than point multiplication. -

2. Key generation

We want to keep our bitcoins safe, so we probably want to control them with at least two different private keys. One is used on a laptop or mobile phone (online wallet, hot wallet) and the other is kept in a hardware wallet/cold wallet. Even if one of them leaks, we still control our bitcoins.

Currently, the way to implement such a wallet is through a 2-2 multi-signature script. That is, a transaction needs to contain two independent signatures.

With Schnorr signatures, we can take a pair of keys (pk1,pk2) and generate a common signature using a shared public key P = P1 + P2 = pk1 * G + pk2 * G. When generating the signature, we need to generate a random number (k1, k2) on the two devices, and generate two random points Ri = ki * G, and add hash(P, R1 + R2, m ), you can get s1 and s2 (because si = ki + hash(P, R, m)* pki ). Finally, add them all up to get the signature (R, s) = (R1+R2, s1+s2), which is our shared signature, which can be verified with the shared public key. Nobody else can tell if it's an aggregated signature, it looks just like a normal Schnorr signature.

However, there are three problems with this approach.

The first problem is on the UI. To initiate a transaction, we need to initiate multiple rounds of interactions on two devices - for computing the common R, and for signing. In the case of two private keys, we only need to visit the cold wallet once: we can prepare the transaction to be signed in the hot wallet, select k1 and generate R1 = k1 * G, and then put the transaction to be signed together with these data Pass in the cold wallet and sign it. Because there is already R1, the signature transaction can be completed in only one round in the cold wallet. From the cold wallet we get R2 and s2 and send it back to the hot wallet. The hot wallet uses the aforementioned (k1, R1) signature transaction, and the sum of the two signatures can broadcast the transaction to the outside world.

This experience is no different from what we can do now, and every time you add an additional private key, the problem will become more complicated. Suppose you have a wealth that is jointly controlled by 10 private keys, and the 10 private keys are stored in different parts of the world. How troublesome it is for you to send transactions at this time! In the current ECDSA algorithm, you only need to visit each device once, but if you use Schnorr's key aggregation, you need to visit twice to get all Ri and sign. In this case, instead of aggregation, it might be better to sign with each private key individually - so that only one round of interaction is required.

After the article was finished, I got feedback from Manu Drijvers: In a provably secure multi-signature scheme, you need 3 rounds of interaction:

• Choose a random number ki and the corresponding random point Ri = ki \G, then tell each device Ri's hash value ti=hash(Ri), and then each device can ensure that you do not know other people's random numbers change idea*

• sign

• sign

The second problem is the known Rogue key attack. The paper explains it very well, so I won't go into details. It probably means that if one of your devices is hacked (for example, your hot wallet is hijacked) and pretends that your public key is (P1 - P2), you can control the shared private key of the two private keys only with the private key pk1 funds. A simple solution is to require a private key to sign the corresponding public key when setting up the device.

There is a third major problem. You can't sign with deterministic k. If you use deterministic k, a hacker can get your private key with just one simple attack. Here's the attack: Some hacker hacks into your laptop and takes full control of one of the private keys (say pk1). We feel the funds are still safe, because using our bitcoin requires an aggregated signature of pk1 and pk2. So we initiate a transaction as usual, prepare a transaction to be signed and R1, send it to our hardware wallet, and after the hardware wallet signs it, send (R2, s2) back to the hot wallet... Then, the hot wallet made an error, Unable to complete signing and broadcasting. So we try again, but this time the hacked computer uses another random number - R1' . We signed the same transaction in our hardware wallet and sent (R2, s2') back to the hacked computer. This time, there's no more - all our bitcoins are gone.

In this attack, the hacker obtained two valid signatures of the same transaction: (R1, s1, R2, s2) and (R1', s1', R2, s2'). This R2 is the same, but R = R1 + R2 and R' = R1' + R2 are different. This means that the hacker can calculate our second private key: s2-s2'=(hash(P,R1+R2,m)-hash(P,R1'+R2,m))⋅pk2 or pk2 =(s2-s2')/(hash(P,R1+R2,m)-hash(P,R1'+R2,m)). I find this to be the most inconvenient part of key aggregation - we have to use a good random number generator every time in order to aggregate securely.

3. Musig

MuSig solved one of the problems - rogue key attacks would no longer work. The goal here is to aggregate signatures and public keys from multiple parties/multiple settings without requiring you to prove that you have the private keys corresponding to those public keys.

The aggregated signature corresponds to the aggregated public key. But in MuSig, instead of adding the public keys of all co-signers directly, we multiply them by some parameters, so that the aggregated public key P = hash(L,P1)×P1 + ... + hash(L,Pn) ×Pn. Here, L = hash(P1,...,Pn) - this public number is based on all public keys. The nonlinear property of L prevents an attacker from constructing a special public key to launch an attack. Even if the attacker knows what his hash(L,Patk)×Patk should be, he can't deduce Patk from it—it's the same as you want to deduce the private key from the public key.

The other processes of signature construction are very similar to those described above. When generating a signature, each co-signer chooses a random number ki and shares Ri = ki * G with others. Then they add up all the random points to get R=R1+…+Rn , and then generate the signature si = ki + hash(P,R,m) ⋅ hash(L,Pi) ⋅ pki . Thus, the aggregated signature is (R, s)=(R1+…+Rn, s1+…+sn) , and the way to verify the signature is the same as before: s×G = R + hash(P,R,m)×P .

4. Merkle tree multi-signature

You may have also noticed that MuSig and key aggregation require *all signers to sign a transaction*. But what if what you want to do is a 2-3 multi-signature script? Can we use signature aggregation at this point, or do we have to use the usual OP_CHECKMULTISIG and sign separately? (Translator's Note: OP_CHECKMULTISIG is the operation code for Bitcoin to verify the elliptic curve multi-signature script)

Let me start with the answer, yes, but the agreement will be slightly different. We could develop an opcode similar to OP_CHECKMULTISIG, except that it checks whether the aggregate signature corresponds to an element on the public key Merkle tree.

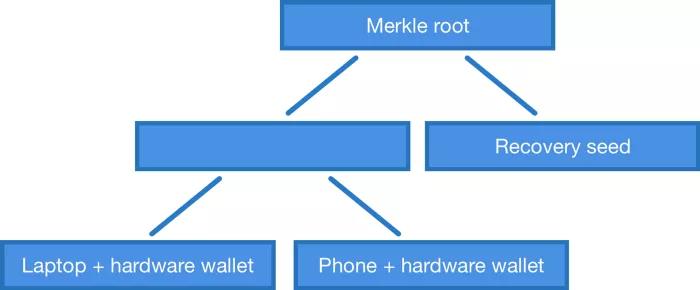
For example, if we want to use public keys P1, P2 and P3 to form a 2-3 multi-signature script, we need to use all pairs of these public keys (P1, P2), (P2, P3), (P1, P3) to build a Merkle tree and publish the root of the Merkle tree in the locking script.

text

But with a Merkle public key tree, we don't have to be limited to mn multi-signature scripts. We can make a tree using any combination of public keys. For example, if we have a laptop, a phone, a hardware wallet, and a mnemonic, we can build a Merkle tree that allows us to use a laptop + hardware wallet, phone + hardware wallet, or a separate Memorize words to use Bitcoin. This is what the current OP_CHECKMULTISIG can't do - unless you use "IF - Else" style flow control to construct more complex scripts.

in conclusion

Schnorr signatures are great, they solve some of the computational overhead in block verification and also give us key aggregation. The latter is somewhat inconvenient to use, but we're not forcing people to use it - we can still use normal multi-signature schemes anyway, using individual, non-aggregated signatures.

I can't wait to use Schnorr signatures, hopefully the Bitcoin protocol will incorporate them soon.

(over)

(over)